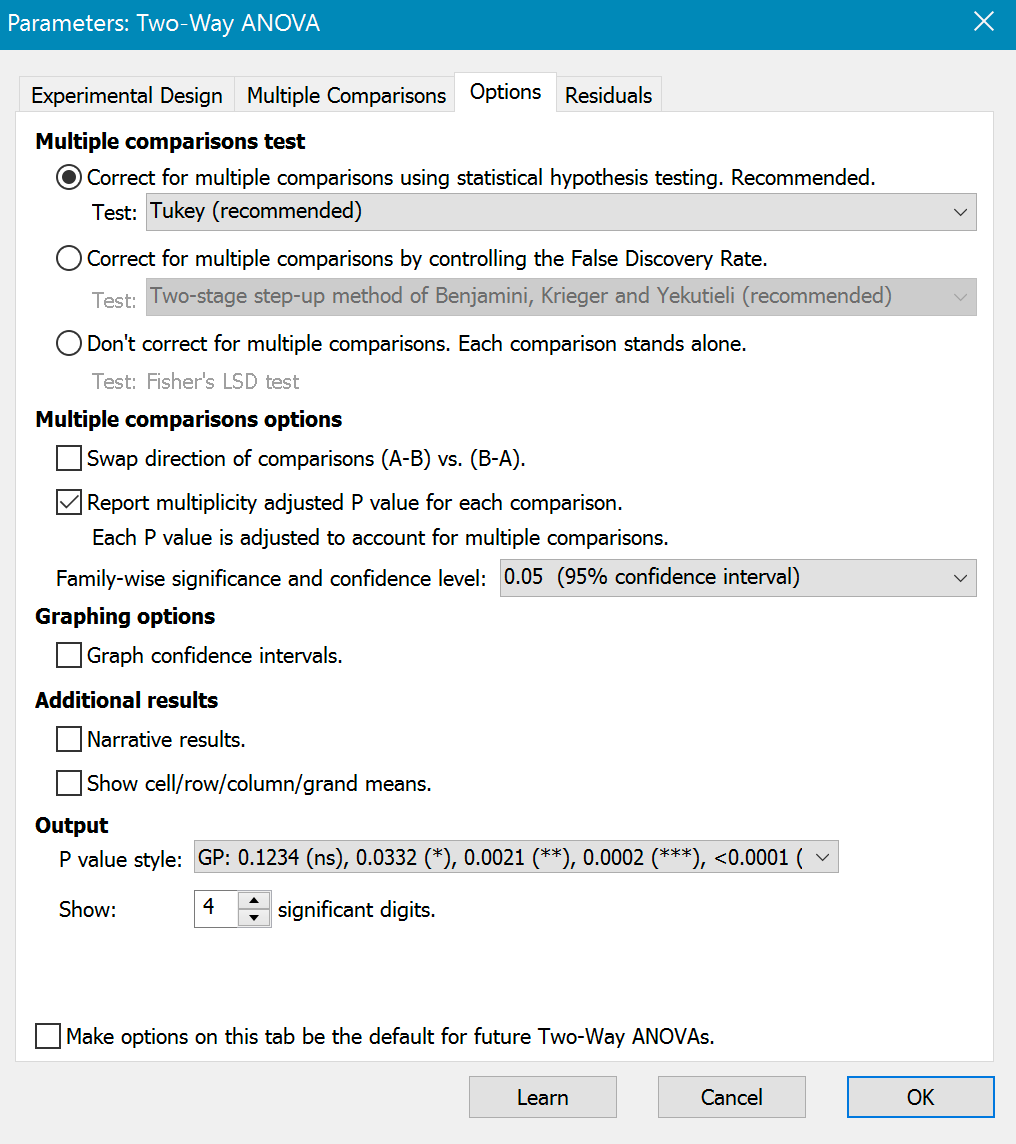
利用统计检验纠正多重比较
在这些方法中,有些可以计算置信区间和多重性调整 P 值,有些则不行。我们推荐使用其中一种可计算置信区间和多重性调整 P 值的检验方法,原因有二:
•对于大多数人来说,置信区间比统计学显著性声明更容易解读。
•多重性调整后的 P 值提供了更多信息,而不仅仅是知道差异是否被认为具有统计学显著性。
推荐方法
可用的检验列表取决于您在第二个选项卡中指定的目标。我们推荐这些检验,因为它们可以计算置信区间和多重性调整 P 值
•如果您要比较每一行(或列)均值与其他每一行(或列)均值,我们推荐使用Tukey 检验。
•如果您要比较一个对照行(或列)均值与其他行(或列)均值,我们建议使用邓尼特检验。
•如果您要比较一系列独立比较,我们建议使用Sidak方法,该方法与 Bonferroni 非常相似,但检验力更强一些。
其他可用方法
提供 Bonferroni 和 Sidak 方法是为了与其他程序兼容,但我们认为选择这些检验方法没有任何优势。
如果您不关心置信区间 的 观察和报告,那么选择 Holm-Šídák 检验可以获得更强的 检验力 。在比较所有对均值时,它比 Tukey 方法的检验力更强(3)。也就是说,对于某些数据集,Holm-Šídák 检验法可以发现 Tukey 检验法无法发现的统计学显著差异。 格兰茨说,霍尔姆检验应该比邓尼特检验具有更大的检验力,但据他所知,这一点尚未得到深入探讨(2)。
由于历史原因, Prism 也提供 纽曼-克厄斯检验 (在比较每个均值与其他均值时)(因此用旧版 Prism 制作的文件可以打开),但我们建议您避免使用,因为它不能将族内错误率保持在指定水平(1)。在某些情况下,I 类错误的几率可能大于您指定的α 水平。
通过控制错误发现率纠正多重比较
Prism 提供了三种控制错误发现率的方法。所有方法都能决定将哪些比较(如果有的话)标记为 "发现",并能控制错误发现率小于您输入的 Q 值。
FDR 方法并不常用于方差分析的后续检验,但这并没有很好的理由。
不要进行多重比较校正。每个比较都是独立的。
如果选择这种方法,Prism 将执行Fisher 最小显著性差异 (LSD) 检验。
这种方法(Fisher's LSD)的检验力更强。但它更有可能得出差异具有统计学显著性的错误结论。当您对多重比较进行校正时(费雪 LSD 没有这样做),显著性阈值(通常为 5%或 0.05)适用于整个比较族。而使用费雪 LSD 时,该阈值分别适用于每个比较。
只有在有充分理由的情况下才使用费雪 LSD 方法,并在报告结果时仔细解释您的做法。
多重比较选项
交换比较方向
该选项的唯一影响是改变所有报告的均值差异的符号。如果选中该选项,2.3 的差异将变为 -2.3。如果选中该选项,-3.4 的差异将变为 3.4。这纯属个人偏好,依赖于您对数据的思考方式。
报告每个多重比较的调整后 P 值
如果您选择 Bonferroni、Tukey 或 Dunnett 多重比较检验,Prism 还可以报告多重性调整后的 P 值。如果选中该选项,Prism 就会报告每个比较的调整后 P 值。这些计算不仅考虑了被比较的两个组,还考虑了方差分析中的组总数(数据集列)以及所有组中的数据。
多重比较调整后的 P 值是整个比较族中最小的显著性阈值(α),在这个阈值下,特定的比较将(勉强)被宣布为 "统计学显著"。
直到最近,多重性调整后的 P 值还没有被普遍报告。如果您选择让 Prism 计算这些值,请花点时间确保您了解它们的含义。如果您在出版物或演示文稿中包含这些值,请务必解释它们的含义。
置信水平和显著性水平(或期望的 FDR)
按照传统,置信区间是按照 95% 的置信度计算的,统计学显著性是使用 0.05 的 alpha 值定义的。Prism 允许您选择其他值。如果您选择控制 FDR,请选择 Q 值(百分比)。如果将 Q 设为 5%,则最多有 5%的 "发现 "可能是假阳性。
参考文献
1.SA Glantz,《生物统计学入门》,第六版,ISBN= 978-0071435093。
2.MA Seaman, JR Levin and RC Serlin, Psychological Bulletin 110:577-586, 1991.