什么是平均数的置信区间？

均值的置信区间 (CI) 可以告诉您确定均值的精确程度。

本示例中，您测量了一个小样本（N=5）的体重，并计算出了均值。该均值与总体均值相等的可能性很小。可能的差异大小依赖于样本量的大小和变异性。

如果样本小且变异性大，那么样本平均数很可能与总体平均数相差甚远。如果样本量大且分散程度小，样本平均数可能会非常接近总体平均数。统计计算将样本量和变异性（标准偏差）结合起来，得出总体平均值的 CI。顾名思义，CI 是一个数值范围。

解读均值的置信区间要做哪些假设？

要解读均值的置信区间，必须假设所有数值都是从一个数值按高斯分布的总体中独立随机抽样得到的。如果接受这些假设，那么 95% CI 有 95% 的概率包含真实的总体均值。换句话说，如果你从许多样本中生成许多 95% CI，你可以期望 95% CI 在 95% 的情况下包含真正的总体平均值，而在另外 5% 的情况下不包含总体平均值。

均值的 CI 怎么可能不包括真实均值呢？

下面的上图显示了十组数据集（N=5），这些数据从均值为 100、标准偏差为 35 的高斯分布中随机抽取。下图显示了每个样本平均数的 95% CI。

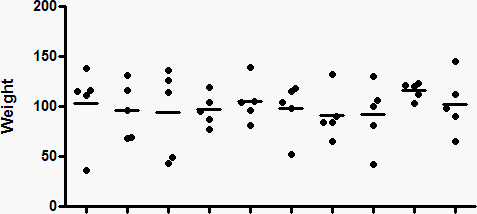
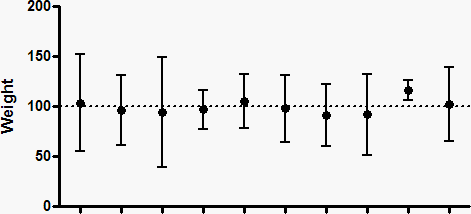
由于这些都是模拟数据，我们知道真实总体均值（100）的精确值，因此可以询问每个置信区间是否包括该真实总体均值。在上图右二的数据集中，95% 置信区间不包括真实均值 100（虚线）。

在分析数据时，由于不知道总体均值，所以无法知道某个置信区间是否包含真正的总体均值。你只知道置信区间包含总体均值的概率为 95%，不包含的概率为 5%。

如何计算平均数的置信区间？

均值的置信区间以样本均值为中心，对称地向两个方向延伸。这个距离等于均值的 SE 乘以 t 分布中的一个常数。该常数的值只依赖于样本量（N），如下所示。

上图中的样本有五个值。因此，其中一个样本的置信区间下限计算为平均值减去 2.776 倍的 SEM，置信区间上限计算为平均值加上 2.776 倍的 SEM。

上表最后一行向您展示了 Excel 中计算乘数的公式。较新的语法是 =T.INV.2T(0.005, N-1)。

一个常用的经验法则是，95% 置信区间是根据平均值加上或减去两个 SEM 计算得出的。对于大样本，该规则非常准确。对于小样本，平均值的置信区间比该经验法则所建议的要宽得多。