置信区间不能量化变异性

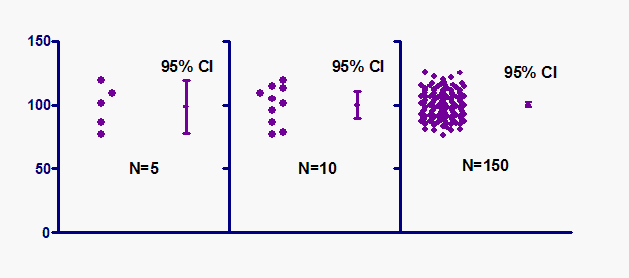
95% 置信区间是一个数值范围，您可以 95% 地确定其中包含了群体的真实平均值。这与包含 95% 数值的范围不同。下图强调了这一区别。

图中显示了三个样本量（大小不同），它们都是从同一个群体中抽取的样本。

左边的小样本，95% 置信区间与数据的范围相似。但在右侧的大样本中，只有极少部分数值位于置信区间内。这是有道理的。95% 置信区间定义了一个数值范围，您可以 95% 地确定其中包含总体平均值。与小样本相比，大样本可以更精确地知道平均值，因此，根据大样本计算出的置信区间是相当窄的。

95%的概率是什么？

正确的说法是，您计算的置信区间有 95% 的概率包含真实的总体均值。说人口平均值有 95% 的概率位于置信区间内则不太正确。

有什么区别？

总体均值只有一个值。你不知道它是什么（除非你在做模拟），但它有一个值。如果你重复实验，这个值不会改变（而且你仍然不知道它是什么）。因此，严格来说，询问种群平均数位于某个范围内的概率并不正确。

相反，你计算的置信区间依赖于你偶然收集到的数据。如果重复实验，置信区间几乎肯定会不同。因此，询问置信区间包含种群平均数的概率是可以的。

而询问人口平均值在区间内的概率则不太正确。要么在区间内，要么不在区间内。这不存在偶然性。你可以说的是，如果你多次进行这样的实验，置信区间不会都是一样的，你会期望其中 95% 的置信区间包含总体平均值，你会期望其中 5% 的置信区间不包含总体平均值，而且你永远不会知道某个实验的置信区间是否包含总体平均值。

95% 并无特别之处

虽然置信区间通常用 95% 的置信度来表示，但这只是一种传统。置信区间可以按照任何需要的置信度来计算。

人们通常会惊讶地发现，99%置信区间比 95% 置信区间更宽，而 90% 置信区间则更窄。但这是完全合理的。如果你希望置信区间包含真实参数的置信度更高，那么置信区间就会更宽。如果您想 100.000% 确定一个区间包含真实的人口，那么它就必须包含所有可能的值，因此区间就会非常宽。如果您只愿意有 50%的把握认为区间包含真实值，那么区间就可以窄很多。