本指南将指导您使用 Prism 执行多重逻辑回归。逻辑回归是 Prism 8.3.0 新增的功能
数据
首先,我们要在欢迎对话框中创建一个新的多重变异性数据表
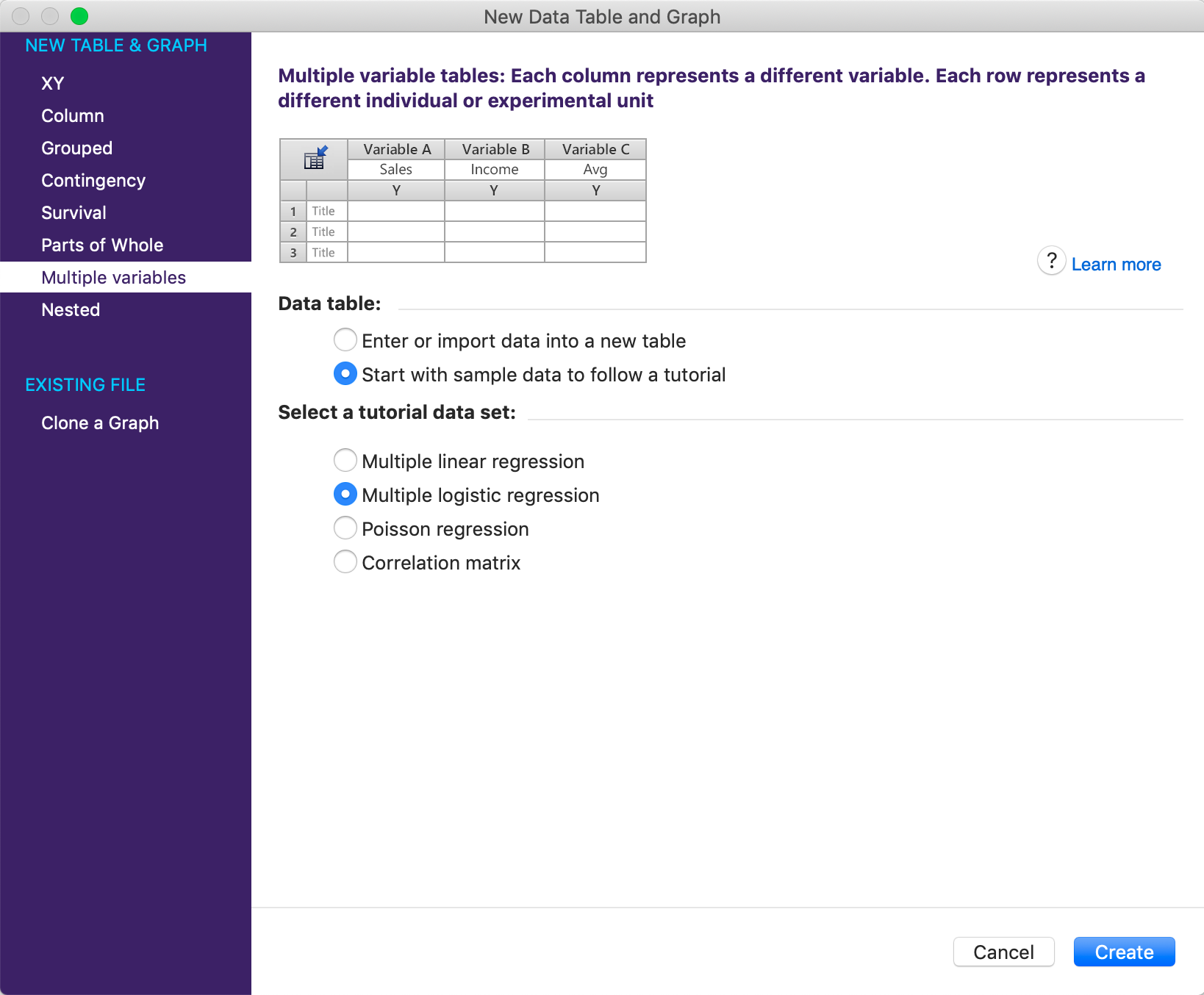
在多变量数据表的教程数据集列表中选择多重逻辑回归样本数据。
样本数据共有五列:"存活?"、"年龄(岁)"、"男性?"、"一等舱?"和 "二等舱?"。
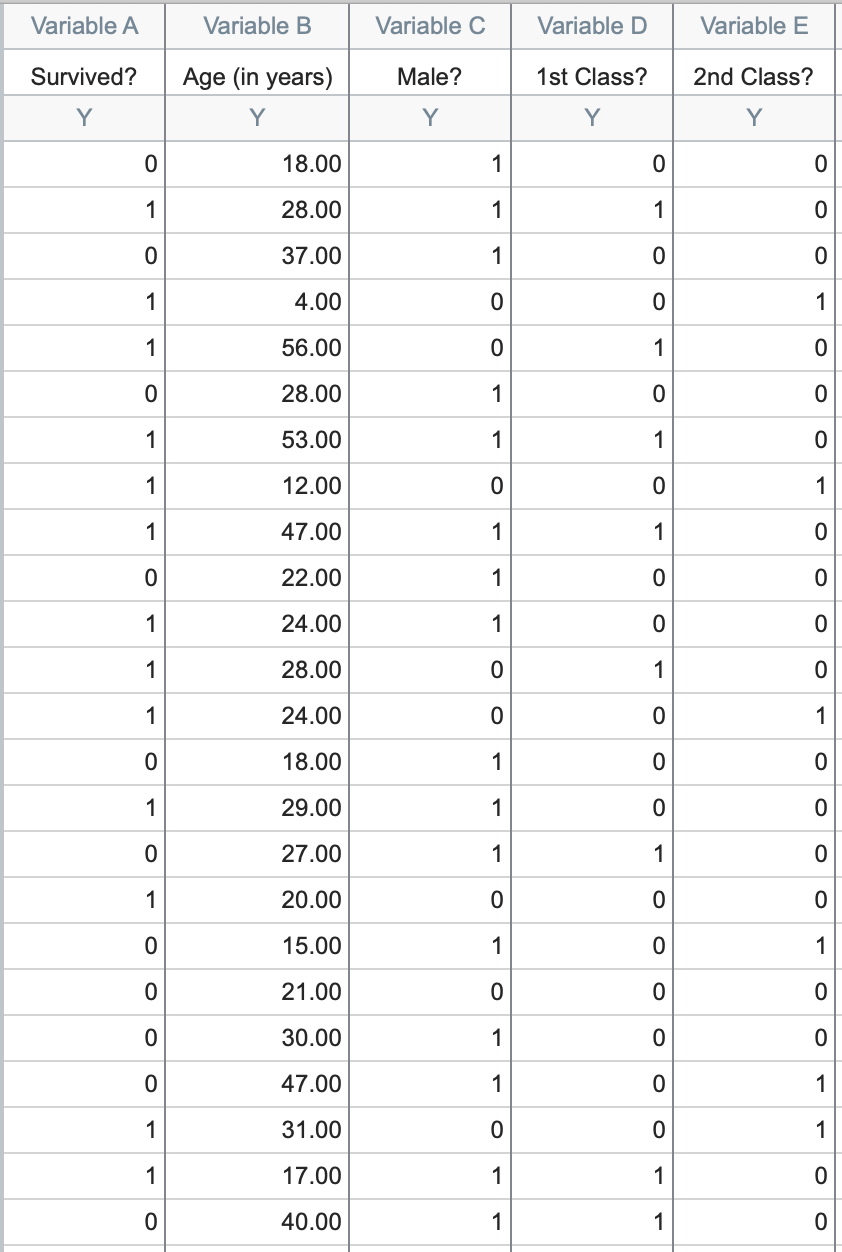
这些数据代表了泰坦尼克号邮轮上的 1314 名乘客,每一行代表一名不同的乘客(请注意,本数据集中不包括船员,而且不同来源的官方乘客人数也不尽相同)。第一列 "幸存?"提供了每位乘客的命运,1 表示乘客幸存,0 表示乘客在船沉时死亡。其他四列提供了每位乘客的人口信息和购票舱位。请注意,这四列中的三列也进行了编码(这些列中的所有值要么为 1,要么为 0)。下文简要说明了编码的工作原理。要直接进行分析,请跳至"启动分析"。
第 3 类怎么办?(虚拟编码快速入门)
如上所述,该数据集中的一些变异性变量被编码为 1 或 0。 在每种情况下,列标题都被输入为一个问题,给定观测值出现 1 意味着该问题的答案是 "是",而观测值出现 0 则意味着该问题的答案是 "否"。例如,我们可以从上表第一行中看出一些关于乘客的信息。第一列中的 0 表示该乘客没有存活,年龄为 18 岁,第三列中的 1 表示该乘客为男性。
但这位乘客的机票等级是什么呢?我们在第四栏看到,该乘客不是一等舱,在第五栏看到,该乘客不是二等舱(这两栏都是 0)。因此,我们可以得出结论,这位乘客一定是三等舱(因为他不是一等舱或二等舱,而这是唯一的可能性)。
当一个变量是分类变量(幸存/死亡、男性/女性、一等/二等/三等等)时,我们可以将这些回答编码为一组 0 和 1,这个过程称为虚拟编码(还有其他编码技术,但虚拟编码可能是最容易理解的)。使用虚拟编码,具有两种结果(存活/死亡、男性/女性等)的变异性变量最终只需使用一列进行编码。您不需要一栏写 "男性?",一栏写 "女性?",因为您可以从一栏中获取所有信息。同样,具有三种结果(一等/二等/三等)的变异性最终使用两列进行编码。在这种情况下,我们不需要 "三等?"这一列,因为我们可以从其他两列的值中辨别出这一信息。事实上,如果在逻辑回归模型中加入 "3rd Class "一列,分析就会因为变量的线性依赖度而失败。
启动分析
单击工具栏中的多重逻辑回归按钮(如下图所示),或单击工具栏中的 "分析 "按钮, 然后从可用的多变量分析列表中选择 "多重逻辑回归"。
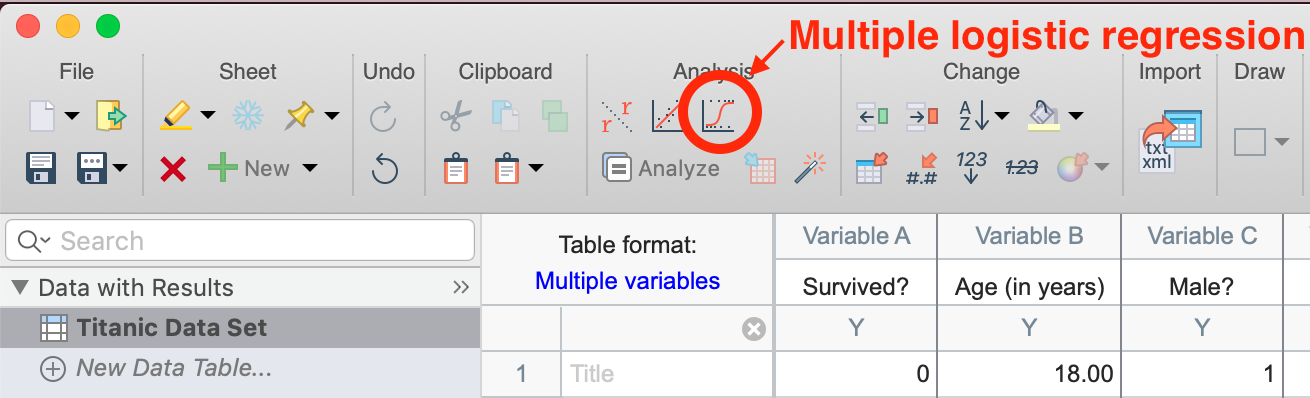
分析对话框
单击多重逻辑回归按钮后,将出现该分析的参数对话框。在本教程中,我们只需接受大部分默认选项。下文将讨论这些默认选项的结果,但多重逻辑回归参数对话框的每个选项卡上还有更多可用选项。为了便于解释结果,我们将对 "负结果 "和 "正结果"(即输入的响应为 0 或 1 意味着什么)的标签进行更改。在 "负面结果 "标签的空格中输入 "死亡",在 "正面结果 "标签的空格中输入 "存活"。
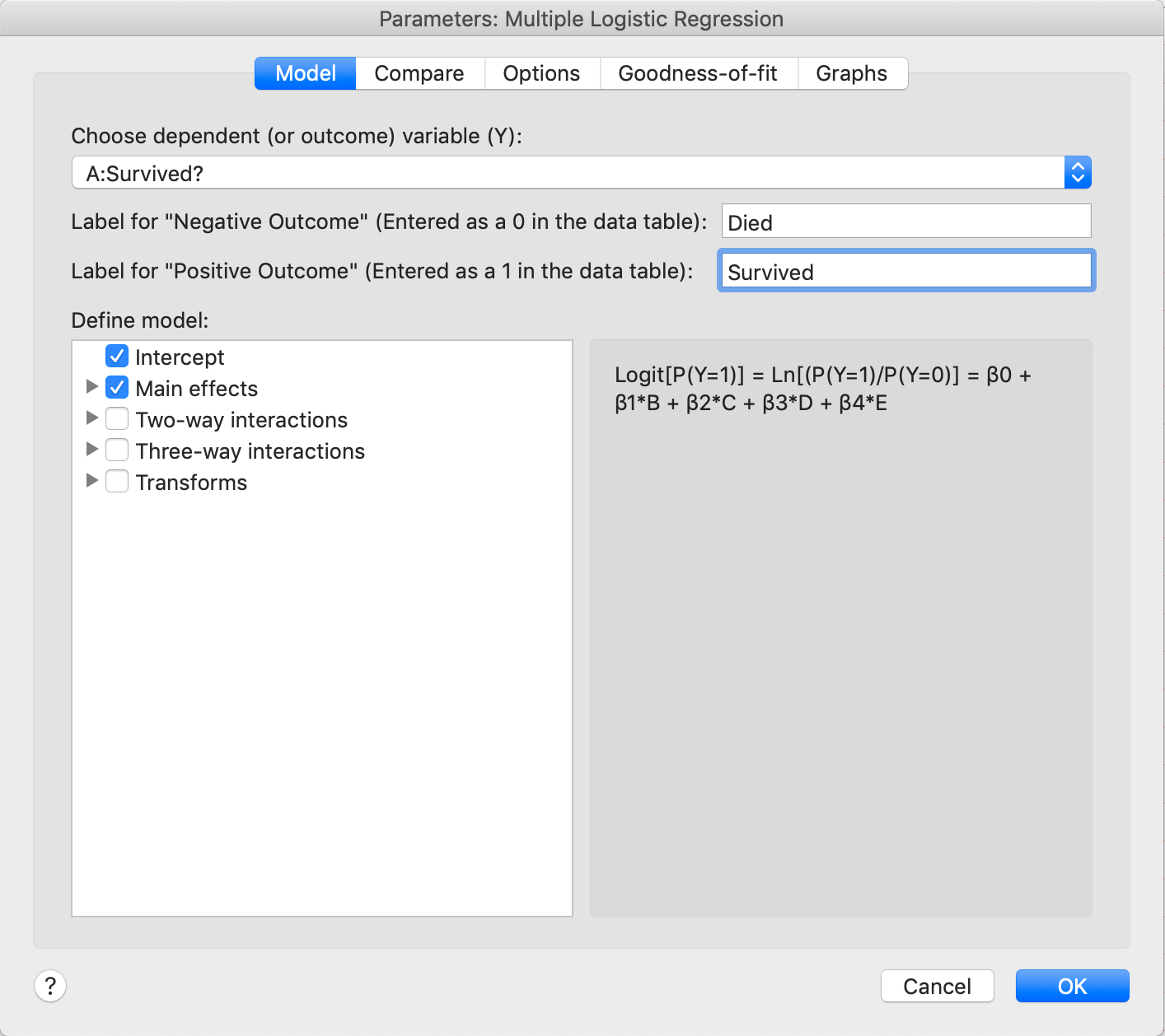
点击 "确定 "后,您将进入主结果表,下一节将讨论该表。
逻辑回归结果
参数估计
在结果表单上首先看到的是β0 的拟合优度值估计以及标准误差和 95% 置信区间,同时还有模型中每个成分(主效应或交互作用)的一个参数估计。在本例中,我们有截距(β0)和四个主效应的参数估计。
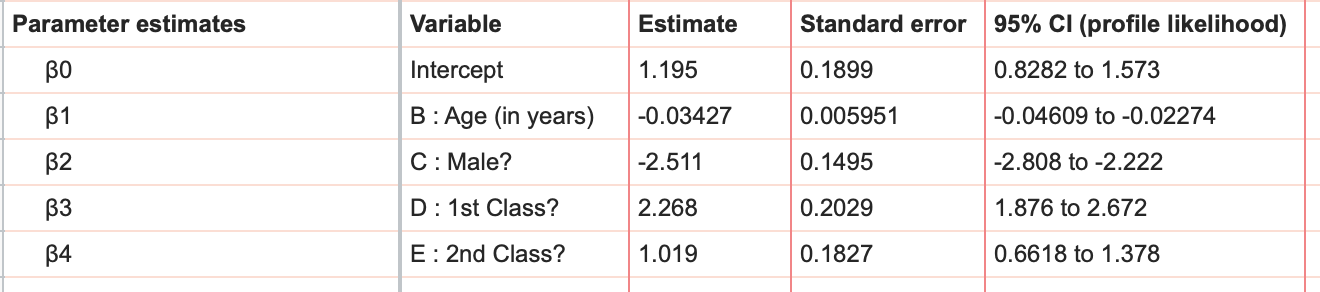
对这些参数的解读与线性回归有些不同,这是因为逻辑回归建立的是对数几率模型。在尝试理解这些参数估计之前,请确保您理解了对数几率、几率和概率之间的关系。在本示例中,我们看到 "男性?"的估计值为-2.511,而 "头等舱?"的估计值为 2.268。这意味着,如果乘客是男性(所有其他变量保持不变),他们的生存几率对数减少了 2.511,而如果乘客是头等舱乘客(所有其他变量保持不变),他们的生存几率对数增加了 2.268。
优势比
除了以对数几率显示结果外,Prism 还报告了几率比及其 95% 置信区间(报告在结果表的更下方)。
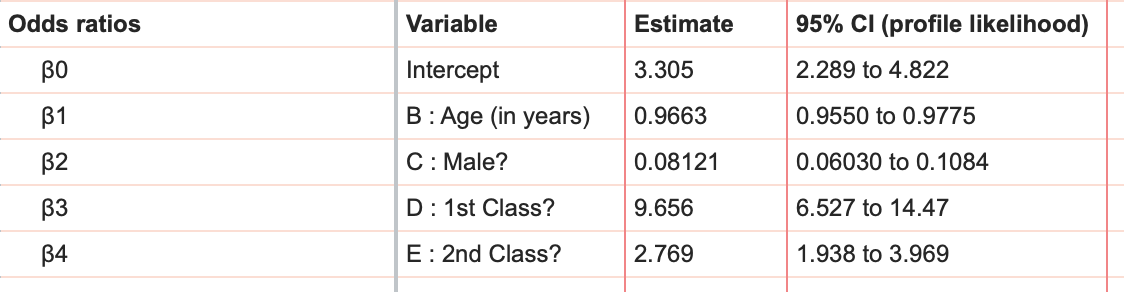
关于优势比的更详细的解释可以在这里找到,但每个变量(β1、β2、β3 和 β4)的优势比告诉我们的是,该变量增加 1,成功的比率就会乘以优势比的值。年龄(岁)"的优势比为 0.9663。这意味着乘客的年龄每增加一岁,其存活几率就会乘以 0.9663。由于该优势比小于 1,这意味着随着乘客年龄的增加,他们的存活几率实际上会降低(所有其他因素保持不变)。
另一点需要注意的是,由于我们对一些变量使用了虚拟编码,因此这些优势比假定了这些乘客的某种 "默认 "或 "参考 "状态。例如,我们可以将变量 "男性?"、"头等舱?"和 "二等舱?"设置为等于零,以调查年龄对生存几率的影响。不过,因为我们使用了虚拟编码,所以我们实际要研究的是年龄对三等舱女性乘客存活几率的影响。假设我们确定的是三等舱女性乘客 25 岁时的存活几率。在这种情况下,"男性?"、"头等舱?"和 "二等舱?"的值都是 0,得出的几率就是 1.402。了解了这一点,我们就可以快速确定 25 岁的头等舱女性乘客的存活几率(Odds = 1.402*9.656 = 13.538)。因此,在使用虚拟编码时,优势比实际上告诉了我们相对于参照案例的几率变化情况。
复习概率和几率
如果您还没有读过概率和几率的关系,这里有一个快速总结:
几率 = 成功概率/失败概率
由于失败的概率仅为 1 - 成功的概率,我们可以将其写为
几率 = (成功概率)/(1 - 成功概率)
本示例中,假设成功概率为 75%,那么几率的计算公式为
几率 = 0.75/(1 - 0.75) = 0.75/0.25 = 3
通常,我们会说 "几率是 3:1"(读作 "三比一")。
P 值
默认情况下,结果中不会给出参数估计的 P 值,因此这里也不会讨论。不过,您可以使用多重逻辑回归参数对话框的选项选项卡选择显示这些值。如果选择让 Prism 报告这些值,还需要阅读如何解读这些值。
模型诊断
多元逻辑回归结果的下一部分提供了许多有用的模型诊断,用于确定数据与所选模型的匹配程度。默认情况下,这里报告的两个值包括 "仅截距模型 "和 "所选模型 "的自由度和校正阿凯克信息准则 (AICc)。这两个模型比较容易描述:
•仅截距模型:逻辑回归模型仅包括截距项 β0。这种模型在预测结果时不使用任何一个自变量。因此,对每个病例的预测结果都是一样的。
•所选模型:您选择拟合数据的逻辑回归模型
本节的结果实际上为您提供了一种方法,可以确定您所选的模型在拟合数据方面是否比 仅截距模型做得更好。另一种说法是,您所选模型中的变异性提供了关于观测数据的有用信息。确定哪个模型能更好地拟合数据的方法是使用 AICc。AICc 的计算方法有点复杂,但在本例中的解读相当简单:AICc 越小,表明模型拟合度越高。仅截距模型的 AICc 值为 1746,而所选模型的 AICc 值为 1235,因此我们可以确定所选模型能更好地描述观察到的数据。
行预测
我们要讨论的下一部分实际上不在主结果选项卡上。在主结果表的顶部,你会看到一个名为 "行预测 "的选项卡。点击该选项卡后,Prism 将为所有观测值提供一份完整的预测概率列表,其中包含每个变量的完整信息:
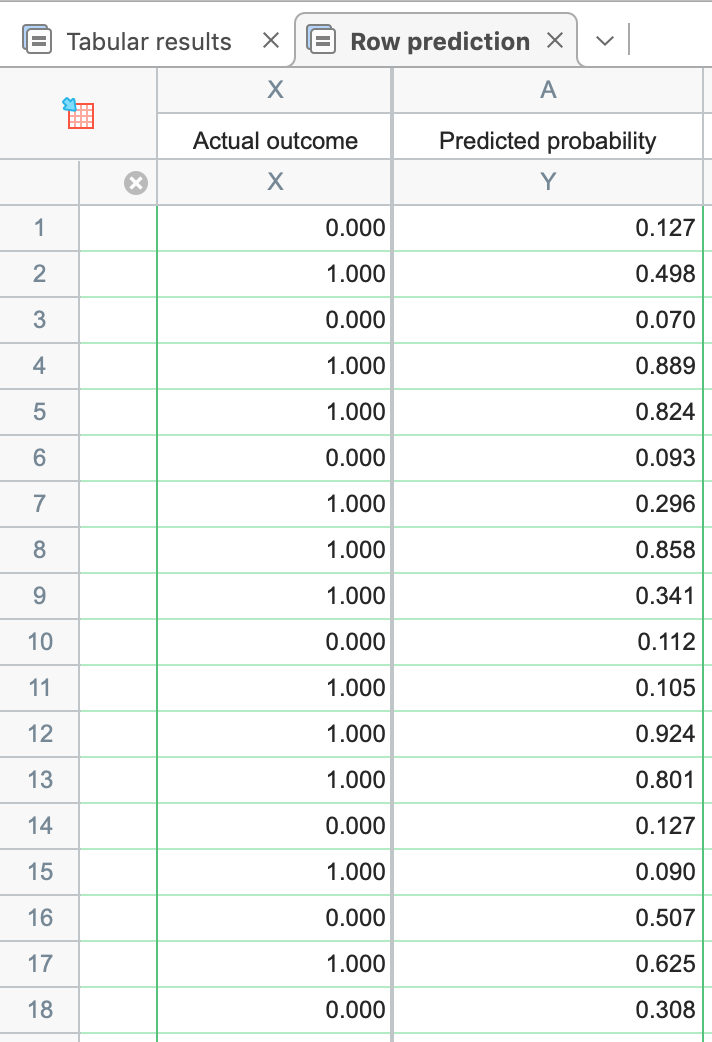
该表提供了表中所有完整观测值的预测概率。这既包括拟合值的数据中的观察值,也包括没有输入 Y 值的观察值。在本示例中,我们可以假设一位男性乘客,年龄 34 岁,持有二等座车票。令人惊讶的是,目前的数据集中并不存在这样的乘客。不过,我们可以在原表第 1315 行的相应变量中输入这名假想乘客的相应值,而将 "存活?"单元格留空。由于生存单元格是空白的,因此在表格中添加这一行不会影响逻辑回归的大部分结果。但是 Prism 会显示这个假设个体的预测生存概率。
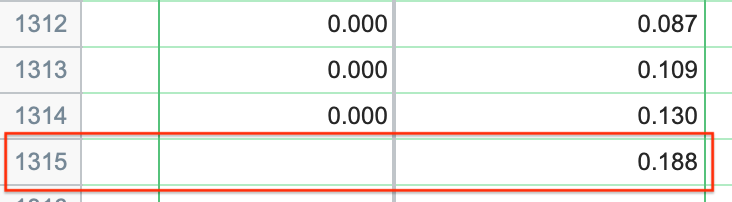
这一结果告诉我们,根据对其他 1314 名乘客的观察,我们的新假设乘客(34 岁,男性,持有二等舱机票)的存活概率仅为 18.8%!
ROC 曲线和 ROC 曲线下面积
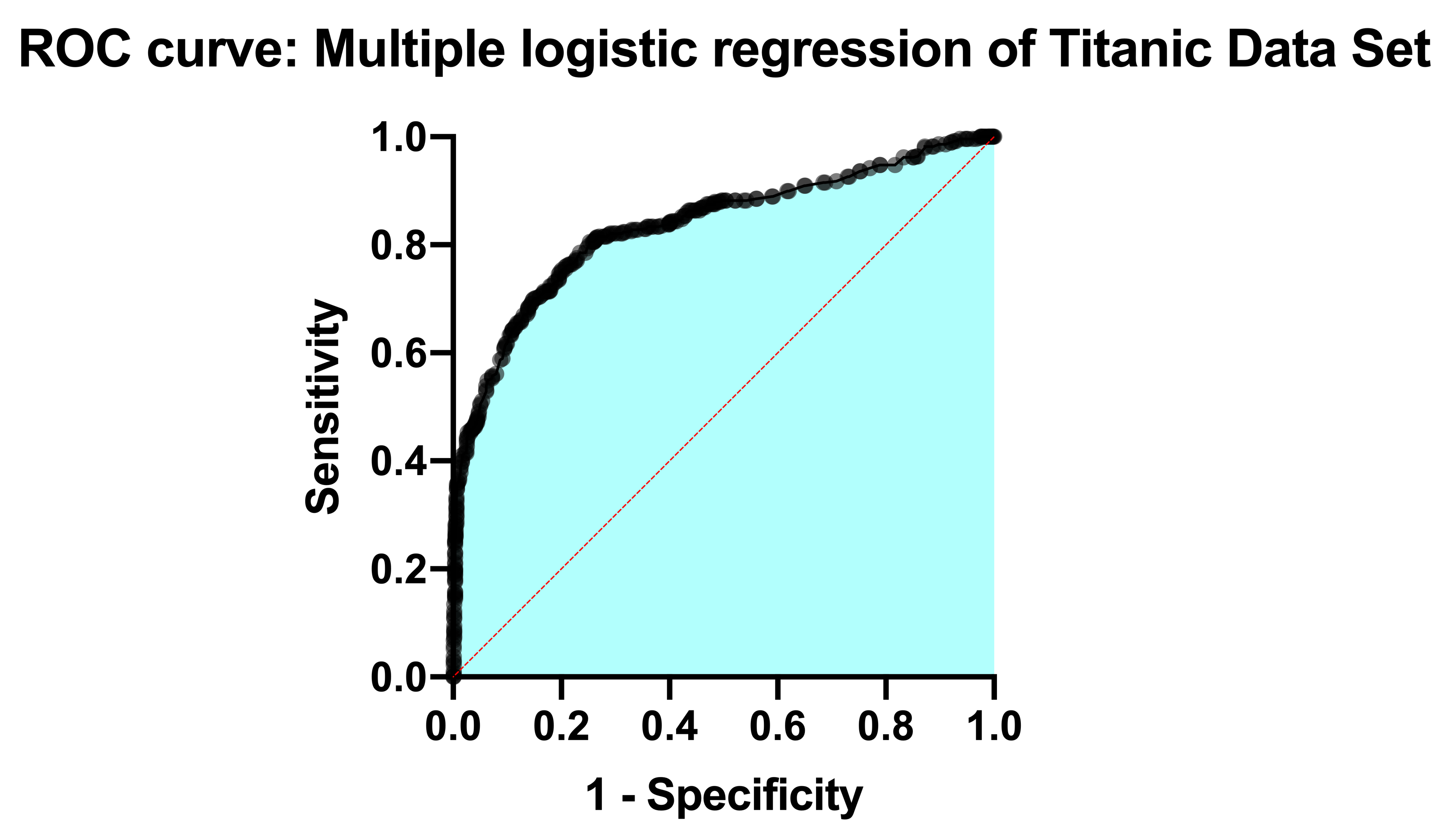
回到结果表的 "表格结果 "部分,结果的下一部分专门讨论 ROC 曲线。该分析的 ROC 曲线在导航器的 "图表 "部分提供,看起来像这样:

理解 ROC 曲线需要一些经验,但这些图表最终向您展示的是模型正确分类成功的能力与正确分类失败的能力之间的关系。模型对观察值进行分类的方法是设置一个临界值。任何大于这个临界值的预测概率都会被归类为 1,而任何小于这个临界值的预测概率都会被归类为 0。如果你设置了一个非常低的临界值,你几乎肯定会将所有观测到的成功概率都正确归类。观察值被正确分类的比例被称为灵敏度,并绘制在 ROC 曲线的 Y 轴上(Y 值为 1 代表成功的完美分类,Y 值为 0 代表成功的完全错误分类)。
不过,如果截断值很低,您也可能会将许多失败的结果错误地归类为成功。特异性是指正确分类失败的比例,"1-特异性 "绘制在 X 轴上(因此,X 值为 0 代表完全分类失败,X 值为 1 代表完全错误分类失败)。
可以想象,随着分界点的变化(从 0 到 1),观察到的成功和失败的正确(和错误)分类将有所权衡。这种权衡就是 ROC 曲线所显示的:随着灵敏度的增加,特异性必然降低(即 1-特异性必然增加)。这条 ROC 曲线上的每一点都代表一个不同的临界值,并具有相应的灵敏度和特异性。
ROC 曲线下面积(AUC)是衡量拟合模型正确划分成功/失败的程度。该值始终介于 0 和 1 之间,面积越大,代表模型的分类潜力越大。在我们的案例中,ROC 曲线(如下图所示)的 AUC 为 0.8889,结果表中列出了 AUC 的标准误差、95% 置信区间和 P 值(零假设:AUC 为 0.5)。阅读更多有关逻辑回归 ROC 曲线的信息,了解更多信息和其中涉及的一些数学知识。

分类表
如上一节所述,ROC 曲线下面积考虑了各种可能的临界值,以区分观察值是预测为 "成功 "还是 "失败"(即预测为 1 还是 0)。在这部分结果中,使用一个临界值来生成一个结果表,提供观察到的 1 和 0 的数量以及预测的 1 和 0 的数量。生成此表的默认截断值为 0.5,但可以在多重逻辑回归参数对话框的 "拟合优度 "选项卡中手动更改。
下表是截断值为 0.5 时的结果:
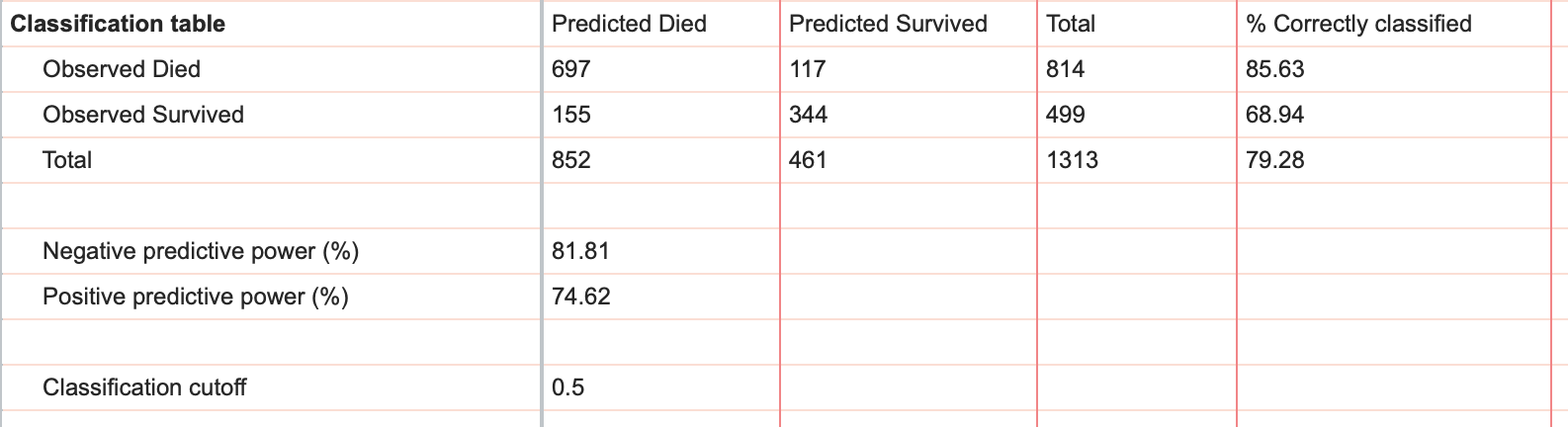
从该表中,您可以快速查看观察到的死亡总人数(814 人)、观察到的存活总人数(499 人)、预测的死亡总人数(852 人)和预测的存活总人数(461 人)。此外,该表还提供了模型预测每种观察到的存活和死亡数的细目,以及正确分类的观察到的存活和死亡数的百分比。
最后,分类表还提供了负检验力和正检验力的信息,这也是评估模型性能的其他方法。
伪 R 平方
量化逻辑回归模型与给定数据拟合值的另一种方法是使用称为伪 R 平方值的指标。需要立即注意的是,虽然名称中可能有 "R 平方",但这些指标的解读方式与线性和非线性回归的 R 平方解读方式完全不同。相反,这些值提供了关于模型拟合的不同信息,其值介于 0 和 1 之间,值越高,表示模型与数据的拟合度越高。
在 Prism 可以计算的各种伪 R 平方值中,Tjur 的 R 平方值可以说是最容易解读的,也是唯一默认报告的值。要计算 Tjur 的 R 平方,需要找出观察到的成功概率的平均预测成功概率和观察到的失败概率的平均预测失败概率。然后计算这两个值之差的绝对值。这就是特优尔 R 平方!接近 1 的值表示观察到的 0 和观察到的 1 之间有明显的分离,而接近 0 的 Tjur's R 平方则表示两组的平均预测成功概率几乎相同(即模型没有很好地分离观察到的 0 和 1)。

预测图与观察图
另一种直观检查所选模型在预测成功和失败方面表现如何的方法是查看导航器的 "图表 "部分默认提供的 "预测与观察 "图表。我们的数据图表如下:
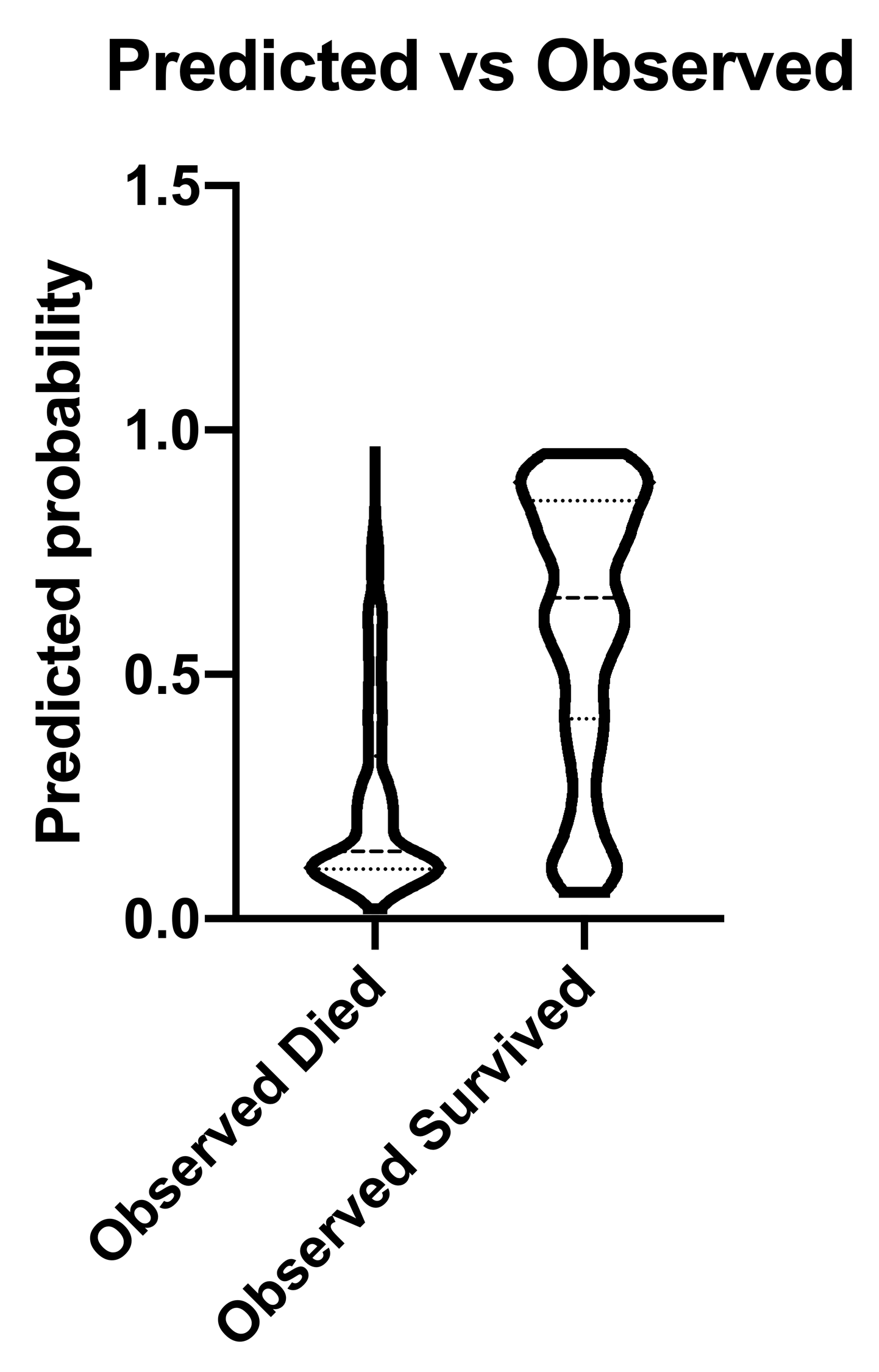
对该图的解读相当直接。在该图中,我们可以看到有两组(一组是存活的个体组,另一组是未存活的个体组)。我们还可以看到这两组的预测概率分布。观察死亡个体组的小提琴图,我们可以看到其中大部分个体的预测存活概率远低于 0.5(中位数为 0.1383,平均值为 0.2411)。我们还可以看到,该模型在对观察到的幸存者群体进行分类时表现不佳。对于该组,我们看到预测概率的分布较为均匀(中位数为 0.6564,平均值为 0.6068)。当然,预测仅基于自变量(年龄、性别和服务等级),忽略了实际结果。
假设检验
如果点击返回结果表的 "表格结果 "选项卡,我们可以继续研究多元逻辑回归报告的其他结果。默认情况下,结果的下一部分提供了Prism 检验模型与数据拟合程度的两种方法之一。这种检验称为 Hosmer-Lemeshow 检验,它检验的是所选模型是否正确的零假设。这个检验的特异性有点复杂,但根据我们的数据,我们很可能会选择拒绝这个零假设,即指定模型是正确的。

鉴于这一结果,我们可能会选择调查可能影响生存概率的其他因素,而这些因素并没有包含在我们最初的模型中。不过,需要注意的是,Hosmer-Lemeshow 检验对其计算方法的细微变化非常敏感,因此在 Prism 的结果中加入该检验主要是为了将 Prism 中的结果与其他应用软件进行验证。
小的 P 值并不一定意味着您的模型本质上 "不好"。毕竟
"所有模型都是错的,但有些模型是有用的......"
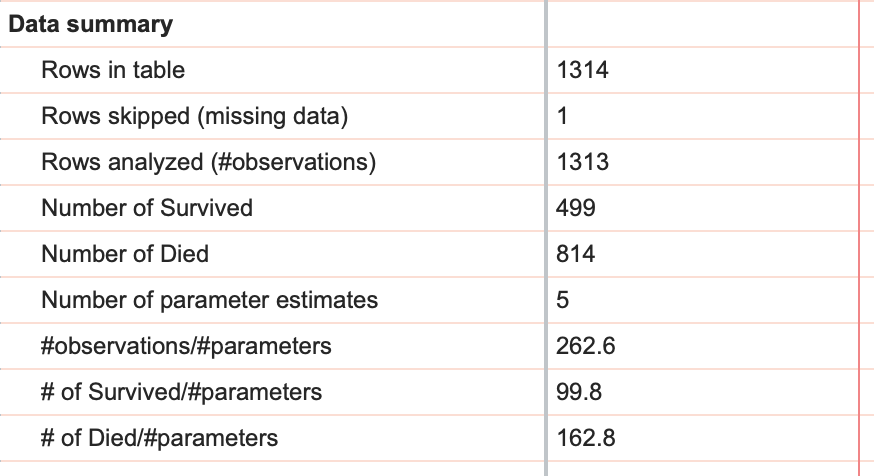
数据总结
Prism 从多元逻辑回归中提供的最终信息是以数据摘要的形式给出的,其中包括数据表中的行数、跳过的行数以及这两个值的差值提供了分析中的观察值。请注意,在我们的数据集中,表中有 1314 行(如果添加本示例进行插值,则为 1315 行),但只分析了 1313 行。造成这种差异的原因是,有一名(或多名)乘客的结果(存活或不存活)是未知的,因此在拟合模型时跳过了这些行。
此外,在数据摘要中,"存活人数 "和 "死亡人数 "分别表示 "1 "和 "0 "的总数。最后,提供了三个比率:观察数与参数数的比率、存活人数与参数数的比率、死亡人数与参数数的比率(我们建议逻辑回归时后两个比率至少为 10)。