回顾逻辑回归模型的拟合过程

将逻辑回归模型拟合到一组数据集的过程包括为模型参数确定一组 "拟合优度 "值。其方法是使用迭代算法最大化逻辑回归模型的似然函数。对这一过程的一种理解是，它试图找出 "最有可能 "产生观察值的模型参数值。这就产生了几个重要的概念。首先，这意味着--一般来说--逻辑回归模型在拟合（或分类）输入数据方面的性能要好于正确预测新数据的结果。

使用这种方法的另一个含义是，在某些情况下，算法无法确定参数值，因此在这些情况下无法定义逻辑回归模型。逻辑回归中常见的三种情况包括：完美分离、准完美分离和 X 变量的线性依赖度。

完美分离

完美分离，有时也称为完全分离，是指一个模型能完美地预测数据。另一种说法是，对于给定的预测因子（或某些预测因子的线性组合），一种结果总是出现在预测因子的某一数值之上，而另一种结果总是出现在该数值之下。这听起来可能有点令人困惑，但实际上它的意思是，模型会正确地将输入为 0 的每个点归类为负结果，将输入为 1 的每个点归类为正结果。表面上看，这似乎不是什么大问题，因为逻辑回归的目标之一就是对观察到的结果进行分类。然而，逻辑回归的另一个目标是找到模型参数的拟合优度估计值，而完美分离的问题在于，在这些情况下，没有一组最佳拟合值可以使可能性最大化。我们来看一个简单的本示例：

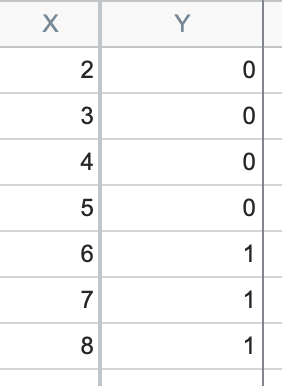
你可以看到，对于每个等于或小于 5 的 X 值，Y 值都是 0；而对于每个大于 5 的 X 值，Y 值都是 1。当只有一个预测因子时（如简单逻辑回归），我们可以从图形上看出完美分离的含义：

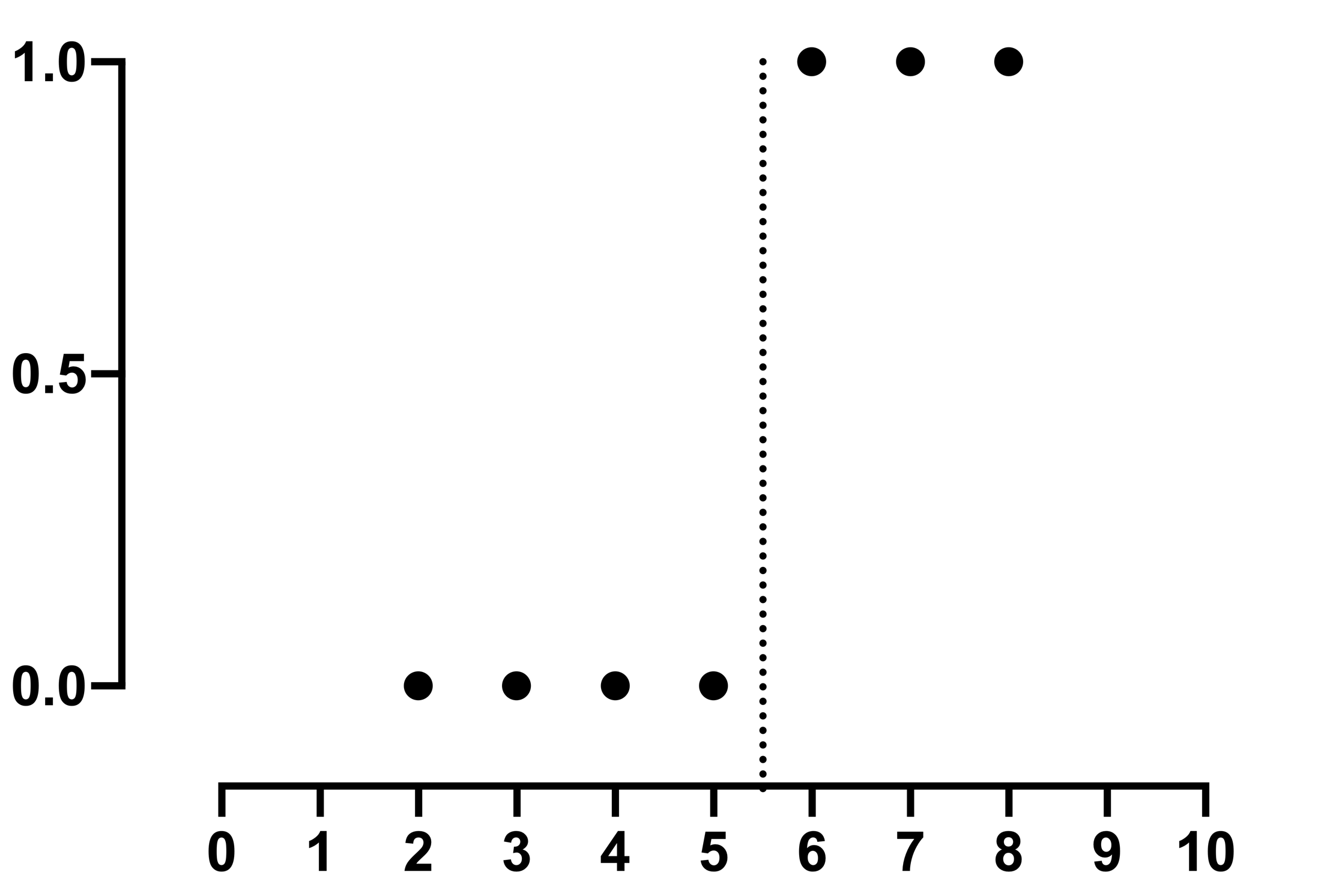
很明显，可以在 X=5 和 X=6 之间画一条垂直线，这条线左边的所有点都在 Y=0 处，而线右边的所有点都在 Y=1 处。但 S 形逻辑曲线却无法预测结果，因为数据没有给出曲线在 5 和 6 之间的位置。如果 X=5.5，预测概率是多少？

准完美分离

准完美分离是一个与完美分离密切相关的问题。它发生在预测因子（或预测因子的线性组合）对结果进行正确分类的情况下，但单个值或点除外。我们再来看看一些数据，以便更好地理解这个问题：

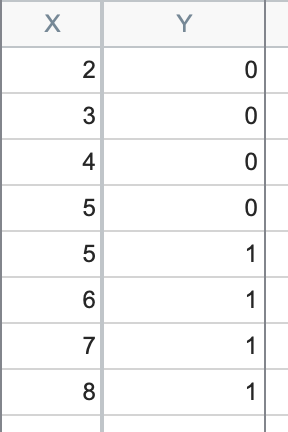
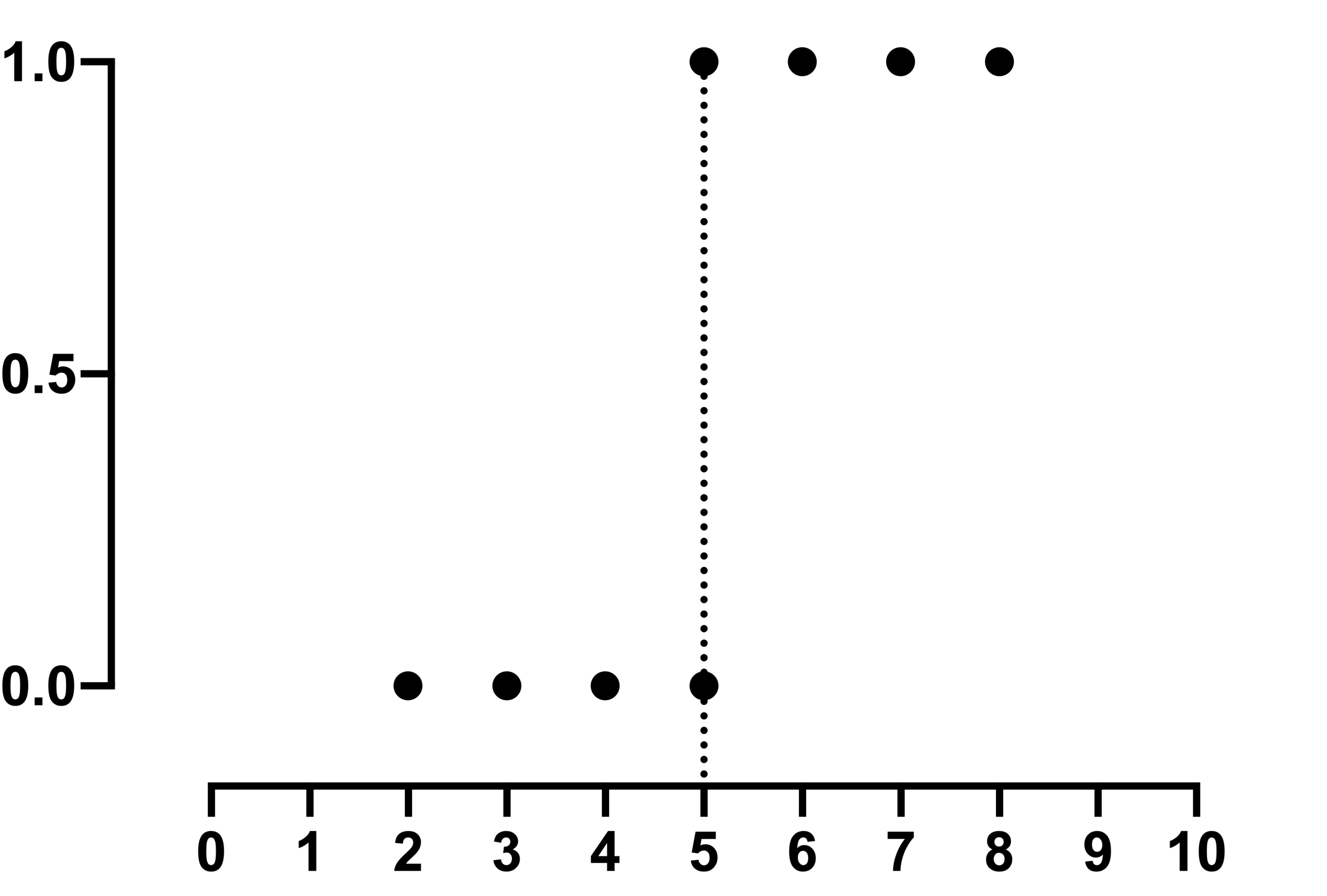
你现在可以看到，对于所有小于 5 的 X 值，Y 值都是 0；而对于所有大于 5 的 X 值，Y 值都是 1。然而，在 X=5 时，我们既有 Y=0 也有 Y=1。再次说明，无法最大化拟合优度，因此无法确定参数的最佳拟合估计值。

最后，如果所有 X 值都是相同的值，Prism 将无法拟合数据的逻辑模型或最大化似然函数（请参阅下文描述线性依赖 X 变量的部分）。

不过，请记住，如果出现这种错误，并不一定代表您的实验设计或数据有问题。这可能仅仅意味着，您已经找到了能够完美（或准完美）预测结果的 X 变异性变量！

线性依赖度 X 变量

在尝试对您的数据拟合逻辑模型时，另一个可能的问题是存在线性依赖性 X 变量。当模型包含线性依赖度预测因子时，拟合模型的算法就会失败，因为似然函数的最大值不存在。要理解这一点，我们先来定义一下线性依赖度的含义。如果你的任何 X 变量都可以表示为其他变量的线性组合，那么就可以说你的变量具有线性依赖度。除非我们也定义一下变量的线性组合的含义，否则这并没有什么帮助。变量的线性组合指的是一组给定变量的总和，每个变量乘以一个常数。本示例可能最容易解释这一点。假设有三个变异性变量：X1、X2 和 X3。现在，我们来写一个公式

X3 = A*X1 + B*X2

如果 A 和 B 的任何值都能使该表达式成立，那么 X3 就是 X1 和 X2 的线性组合。让我们看一些数据来更清楚地说明这个概念：

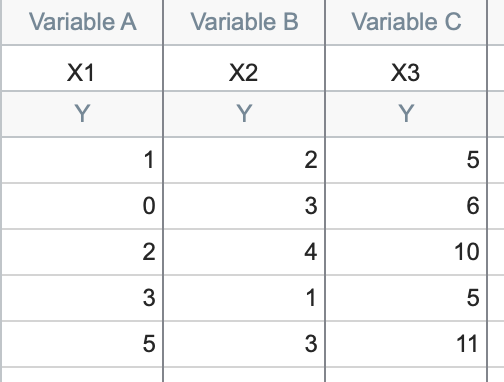
这个数据显示了我们的三个变异性（变异性可以是任何东西：年龄、身高、去卫生间的步数......）。对于这些数据，线性关系很容易发现：

x3 = 1*x1 + 2*x2

换句话说，在每一行中，第三个值都是第一个值加上第二个值的两倍之和。其他线性关系可能不那么容易发现：

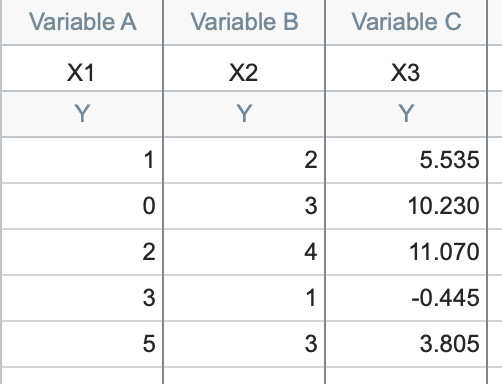
前两列中的数值相同，但这里的线性关系为

x3 = -1.285*x1 + 3.41*x2

线性依赖度问题的另一种表现形式是重复 X 列。在使用已编码的分类预测因子时，可能会无意中出现这种情况。已编码的分类预测因子只能取有限的几个值，因此很容易出现两个原本不相关的分类变量在每个观察值上的值都相同的情况（如果变量在某种程度上相关，这种情况就更有可能发生）。当然，这种偶然发生的几率会随着观察次数的增加而降低。

一个容易理解的两个变量变异性相同的本示例可能来自对足球比赛的分析。想象一下，一个变量代表 "进球数"，而第二个变量可能是 "最终比分"。在这种情况下，这似乎是显而易见的，但您应该始终警惕在模型中伪装成自变量的重复变量（或线性依赖度变量）。

如果您有重复的 X 列、完全相关的 X 列或线性关系更复杂的 X 列，那么优化算法就会失败。要评估这个问题，请使用多重共线性逻辑回归对话框中的多重共线性选项。更多详情，请参阅多重共线性页面。

逻辑回归模型收敛的（部分）潜在问题汇总

1.您的 0 或 1 太少（我们建议，如果可能，每个自变量 (X) 至少各 10 行）

a.在极端情况下，如果您有所有的 0（或所有的 1），就能保证完美分离，因为算法无法区分两种结果。

b.另一种极端情况是，如果您的 X 变异性变量与数据行一样多或更多。这种情况下无法估计模型误差。

2.其中一个 X 变量（或 X 变量的线性组合）会导致 Y 变量的完美分离或准完美分离。

3.您的 X 变量表现出线性依赖度。