在讨论这个问题之前，先来简单回顾一下：

•主成分是原始（标准化/中心化）数据的线性组合

•这些线性组合代表数据可以投射到的线段（降低维度）

•数据可以投射到许多可能的线上

•主成分是通过最大化数据方差来定义的

本节将主要讨论最后一点。请看这里的图像。这张图片代表了一个三维对象的二维投影。仅凭这些信息，我们可能很难知道这个投影所代表的对象是什么。在讨论完如何定义主成分后，我们将再次讨论这个问题。

 

如前几节所述，PCA 是一种在 尽可能保留数据信息的同时降低数据集维度的技术。数据中的 "信息 "由方差给出。考虑一个变量，它的每个观察值都完全相同。这个变量的变异性为零，因此，您无法使用这个变量来区分不同的观测值。对于 PCA 而言，变异性较大的变量包含更多的 "信息"。只需确保您的数据经过适当的转换（通常是通过标准化），这样在不同尺度上测量的变量就不会仅仅因为其测量单位而占主导地位。

因此，PCA 的首要目标是尽可能多地保留 "信息"（方差）。另一个主要目标是确保新的变异性可以用来尽可能 "重建 "原始数据。回想一下，将数据投射到降维空间会导致部分信息丢失，因此无法从降维空间完美地重建原始数据。不过，我们研究了将投影产生的误差最小化的不同方法。也许最重要的是，我们发现通过最小化数据与直线之间的垂直距离所得到的最佳拟合优度线可以同时实现上述两个目标。在 PCA 中，这条最佳拟合线就是第一主成分。

下面是上一节中的两幅图，展示了如何同时实现最小化数据与拟合线之间的距离和最大化拟合线上投影点的方差。左图是拟合线的距离最小化和方差最大化都做得很差。右边的图表显示了实现这些目标的最佳拟合优度线。

 

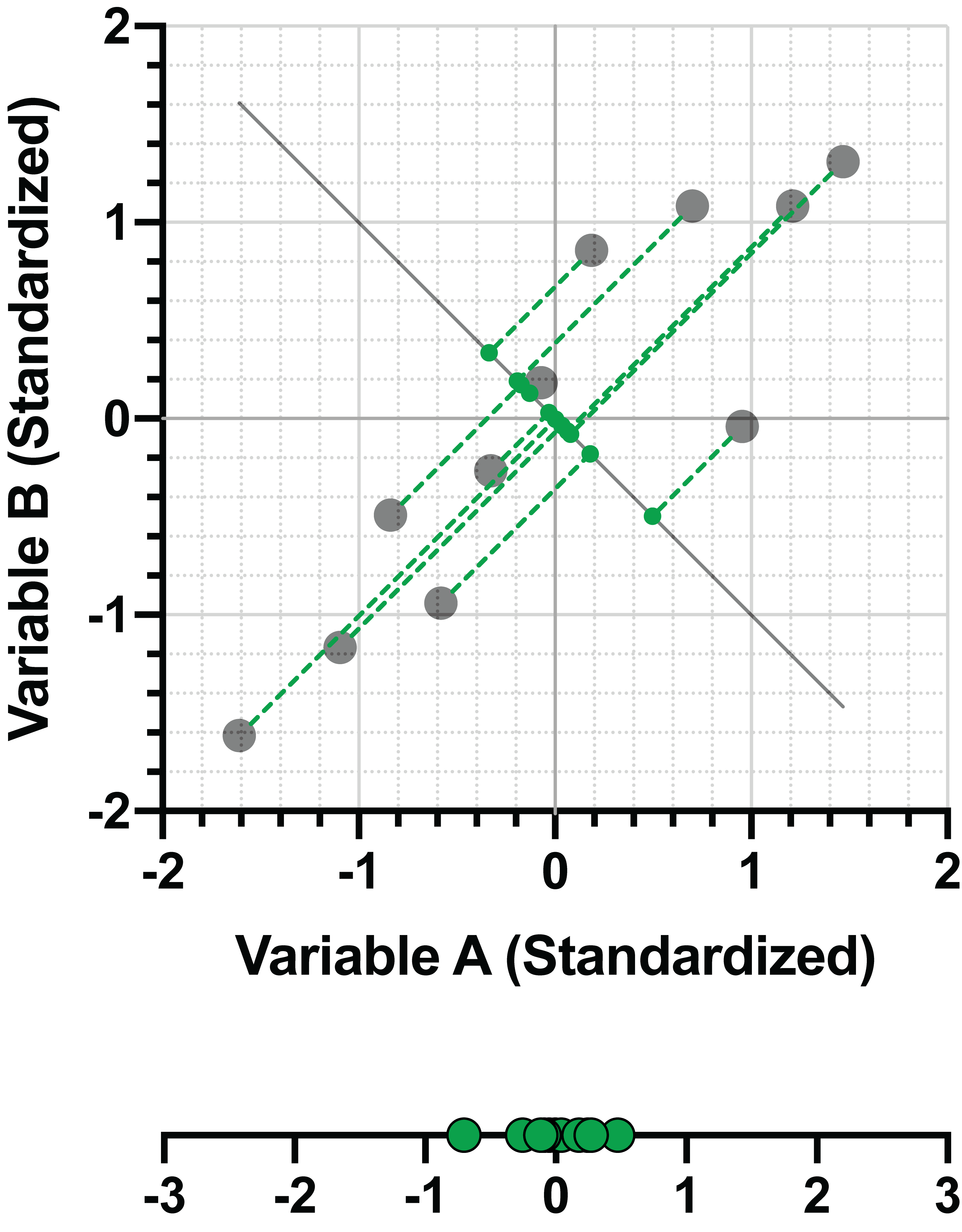
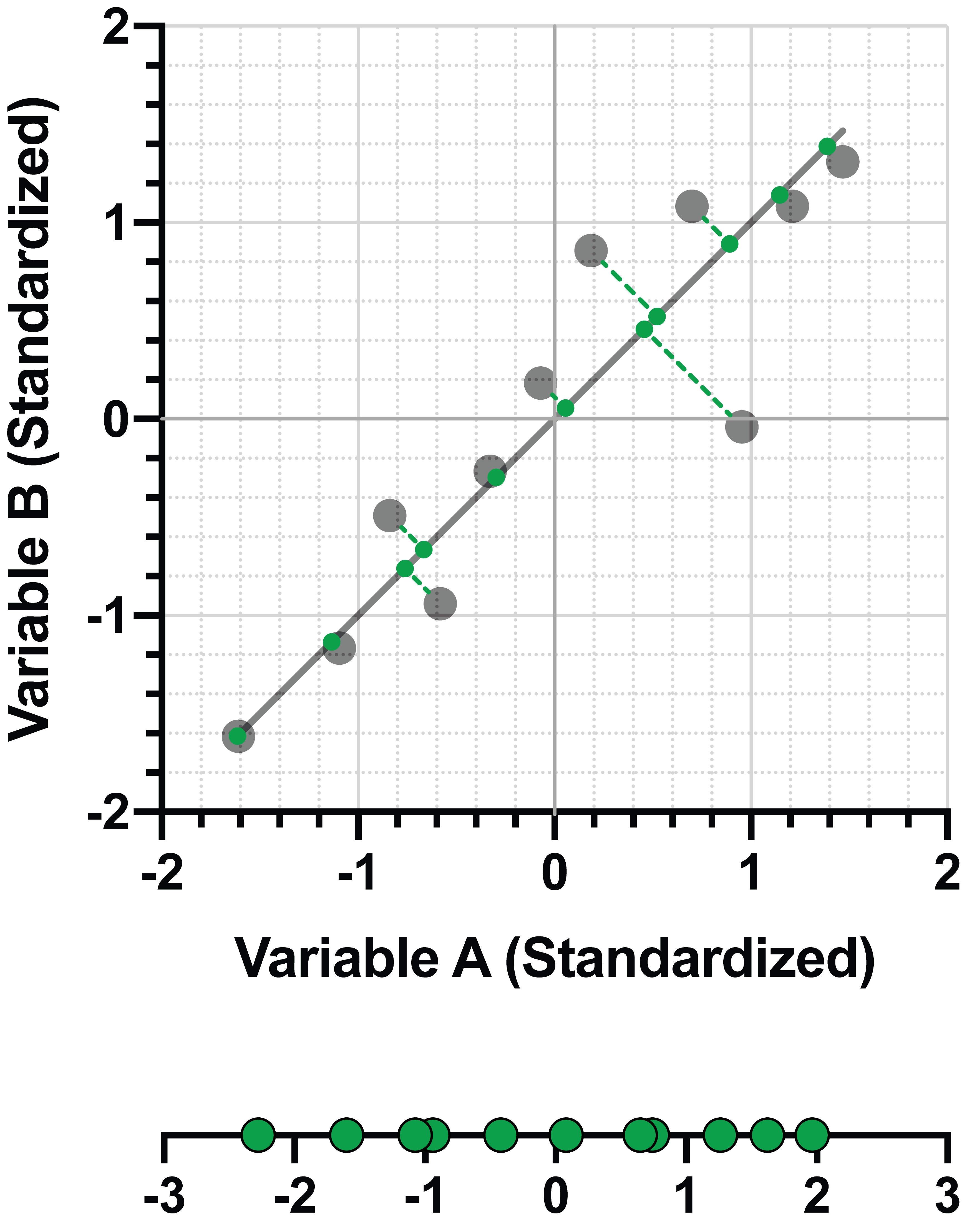
在上本示例的右侧面板中，这条线（我们姑且称之为 PC1，表示 "第一主成分"）可以表示为两个（标准化）变量的线性组合。就本示例而言

PC1 = 0.707*（变异性 A）+ 0.707*（变异性 B）

高级说明：线性组合的系数可以用矩阵表示，这种形式 称为 "特征向量"。该矩阵通常作为 PCA 结果的一部分呈现出来

有了这个公式，我们就有办法用较少的变量（在本例中，只从两个变量减少到一个）来近似（"重构"）原始数据。下表显示了将变异性 A 和 B 的值输入该公式后得到的值：

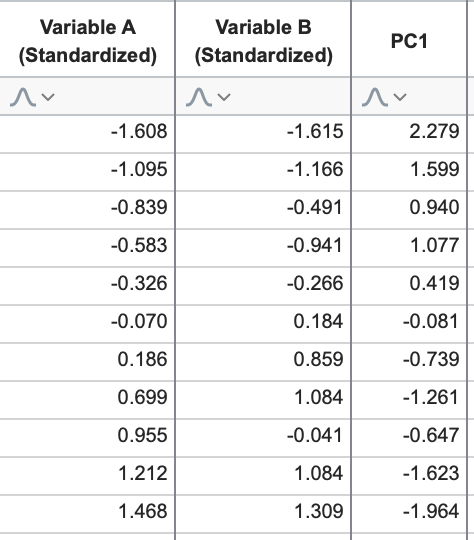
PC1 的这些值被称为 PC1 的 "分数"，代表投影数据在该 PC 上的位置（参见上图右侧图表中的数字线，并与第三列中的值进行比较）。

上面的本示例使用的是一个只有两个变异性的简单数据集。由于 PCA 的目标是降维，我们只寻找了第一个主成分。不过，在下一节中，我们将讨论如何定义其他主成分。

最后一件事。我们现在知道，主成分是通过最大化投影中的数据方差来定义的。为了进一步说明这一点，请看下图：

 

 

这是前面介绍的同一个三维对象的另一个二维投影，我们现在看的应该很清楚了。如果我们把鲨鱼身体的长度看作 X 轴，高度看作 Y 轴，宽度看作 Z 轴，那么这幅图就显示了鲨鱼在 XY 平面上的投影。之前的投影（信息量较少）是同一条鲨鱼在 YZ 平面上的投影。第二个投影之所以更"有信息量"，是因为大部分数据的方差都在 X 轴方向上！我们能够从这种"侧视图"中获得更多信息，因为它保留了原始数据的更多方差，这与 PC 的定义方式相同。

不过，虽然"正面"视图在数据投影方面的信息量可能较少，但这种视图却更能说明你应该游多快......