在上一节中，我们看到第一主成分（PC）是通过最大化投射到该成分上的数据方差来定义的。然而，如果原始数据中存在多个变量（维度），则可能需要添加额外的成分，以保留第一个 PC 无法充分考虑的额外信息（变异性）。

数据可能包含多少个主成分？

一般来说，一个数据集可以用它所包含的变量（列）和观测值（行）的数量来描述。变量的数量通常用p表示（表示 "预测因子"），观测值的数量通常用n 表示。

一个数据集可确定的主成分总数等于 p 或 n，以较小者为准。但有两点需要注意：

•在许多数据集中，p 会大于 n（变异性多于观测值）。这种 "宽"数据对 PCA 来说不是问题，但在多元线性回归或多元逻辑回归等其他分析技术中会造成问题。

•您很少希望保留所有可能的主成分（下一节将详细讨论）。

为简单起见，我们假设所处理的数据集的变异性大于观测值（p > n）。但是，在定义 PC 时，过程是相同的。在确定第一个 PC（使投影到这条线上的数据变异性最大化的变量线性组合）后，下一个 PC 的定义与第一个 PC 完全相同，但有一个限制条件，即它必须与之前定义的 PC 正交。

这在二维空间中很容易理解：两个 PC 必须相互垂直。让我们再次回到变量 A 和 B 的标准化数据。

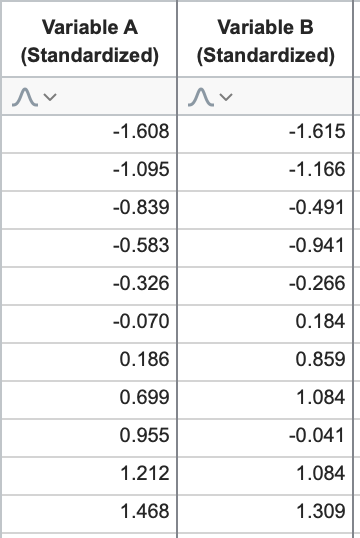
我们知道这些数据的图形如下所示，第一个 PC 可以通过最大化投影到这条直线上的数据的方差来定义（上一节已详细讨论）：

由于我们局限于二维空间，因此只有一条线（绿色）可以垂直于第一 PC：

在前面的章节中，我们已经展示了第二个 PC 如何捕捉到比第一个 PC 更少的投影数据方差：

 

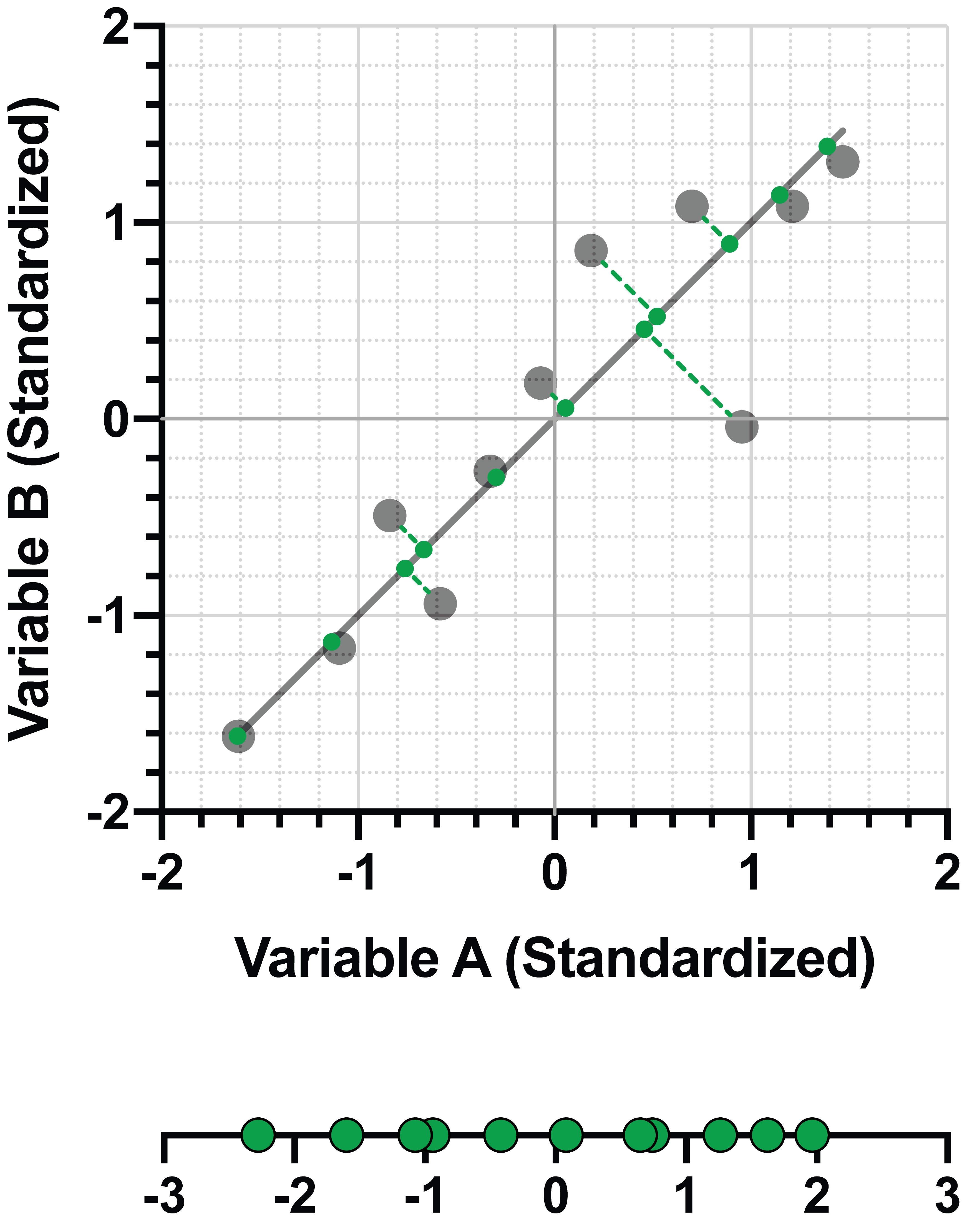
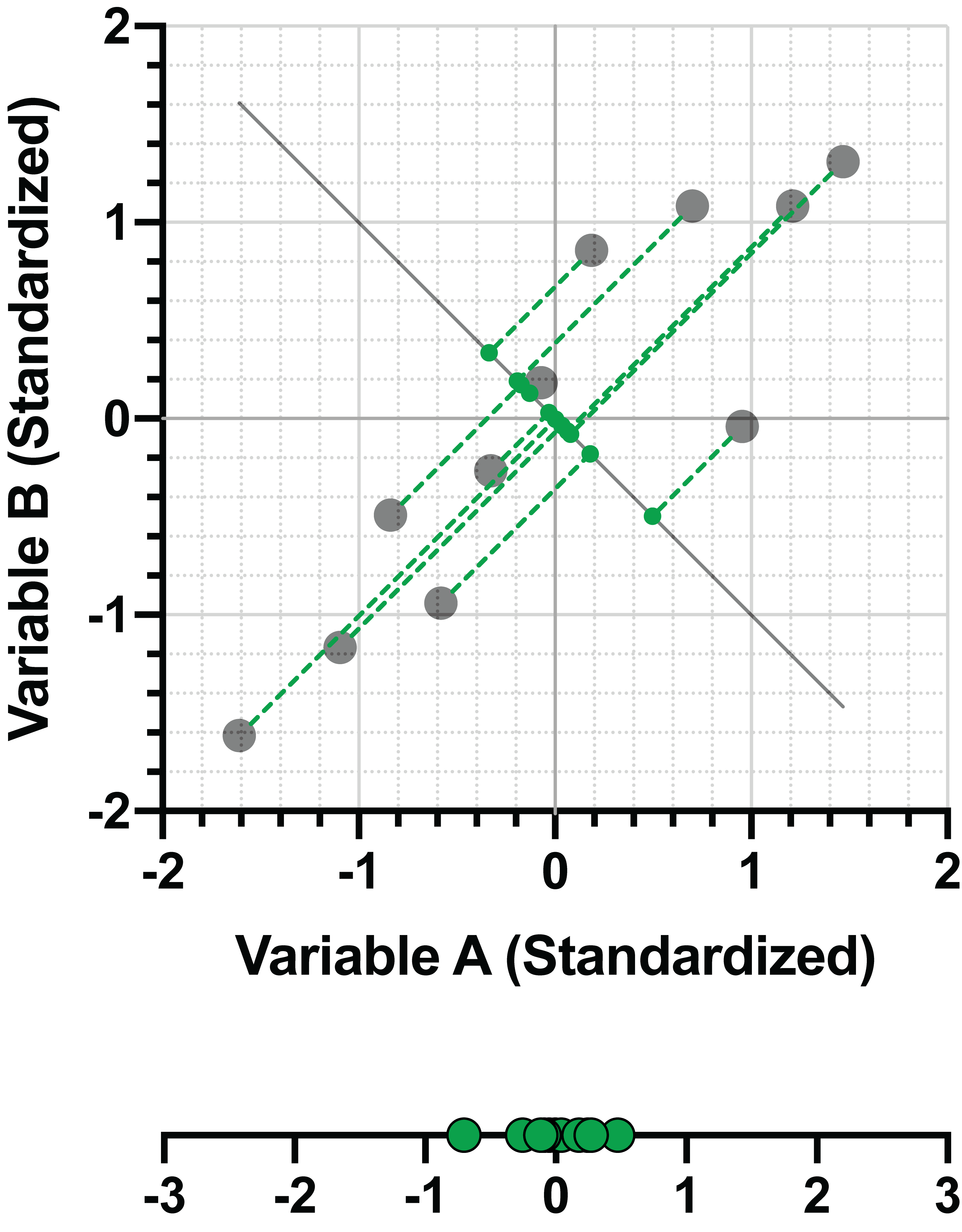
然而，该 PC 可以最大化数据方差，其限制条件是它与第一个 PC 正交。与之前一样，我们可以将此 PC 表示为标准化变量的线性组合。以下是 PC1 和 PC2 的线性组合：

PC1 = 0.707*（变异性 A）+ 0.707*（变异性 B）

PC2 = -0.707*（变异性 A）+ 0.707*（变异性 B）

高级说明：该线性组合的系数可以用矩阵表示，这种形式 称为 "特征向量"。该矩阵通常作为 PCA 结果的一部分呈现出来

利用这种线性组合，我们可以将 PC2 的 "分数 "添加到数据表中：

如果原始数据包含更多变异性，则可以简单地重复这一过程：

•找出一条线，使这条线上的预测数据方差最大。这就是第一个 PC

•找出一条能使该线上的预测数据方差最大，且与之前确定的每个 PC 正交的直线。这就是下一个 PC

在二维空间中将这一过程可视化是非常简单的。理解三维空间中的三条线如何以 90° 角相交也是可行的（考虑一下三维图形的 X、Y 和 Z 轴；这些轴都以直角相交）。然而，随着原始数据维度的增加，可能的 PC 数量也在增加，使这一过程可视化的能力变得异常复杂（试着在 6 维空间中可视化一条与其他 5 条线相交的线，所有这些线都必须以 90° 角相交......）。

幸运的是，识别数据集所有后续 PC 的过程与识别前两个 PC 的过程并无不同。最终，您会得到一个 PC 的排序，第一个 PC"解释"了最大的数据方差，第二个 PC"解释"了次大的数据方差，依此类推。下一节将讨论"解释方差"量是如何呈现的，以及从这些信息中可以做出什么样的决策来实现 PCA 的目标：降维。