下一个选项卡名为 "载荷"，它提供了与本指南之前讨论过但未明确提及的主题相关的信 息。该表以单独一列的形式列出了每个选定 PC 的载荷，并在单独一行中列出了每个原始变异性。虽然单个载荷由一组多个值（每个单独变量一个值）定义，但这些单独值是计算载荷的特异性变量与 PC 之间的相关性。

换句话说，任何给定 PC 的载荷都提供了每个变量与该 PC 相关性的信息。从整体上看，这是另一种观察 PC 与每个原始变量 "吻合"程度的方法。这与 PC 的特征向量概念非常相似。请记住，特征向量代表定义 PC 的变量线性组合的系数。单个特征向量由多个值定义，每个原始变量都有一个系数值。这些系数还提供了 PC 与每个变量的吻合程度的信息：系数越大，表明该变量对 PC 的影响越大。

这就是载荷、特征向量和特征值之间的关系：

特征向量是单位标度的载荷！

要证明这种关系，需要做一些复杂的数学运算，但底线是特征向量的长度为 1，而载荷只是特征向量的 "缩放 "版本。按什么缩放？特征值！严格来说是特征值的平方根。下面是完整的关系

载荷 = 特征向量 * √（特征值）

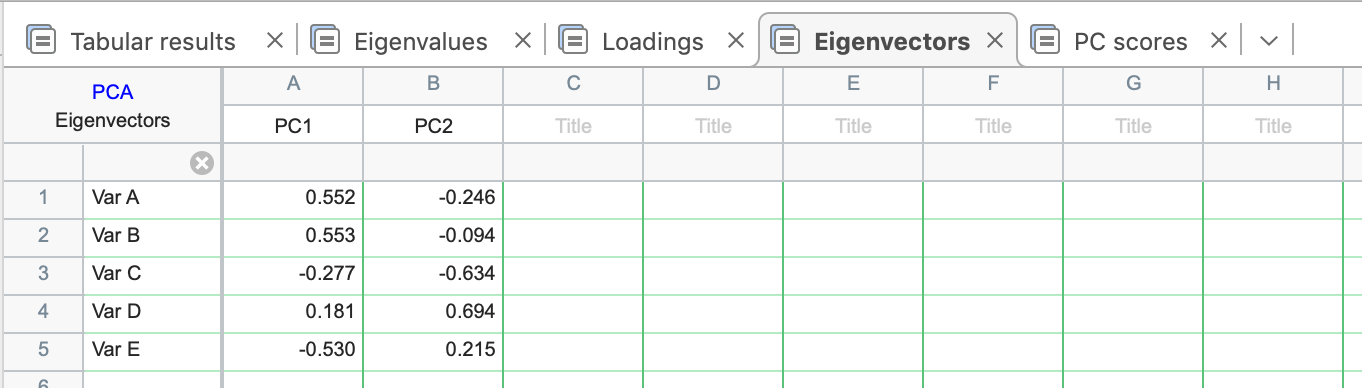
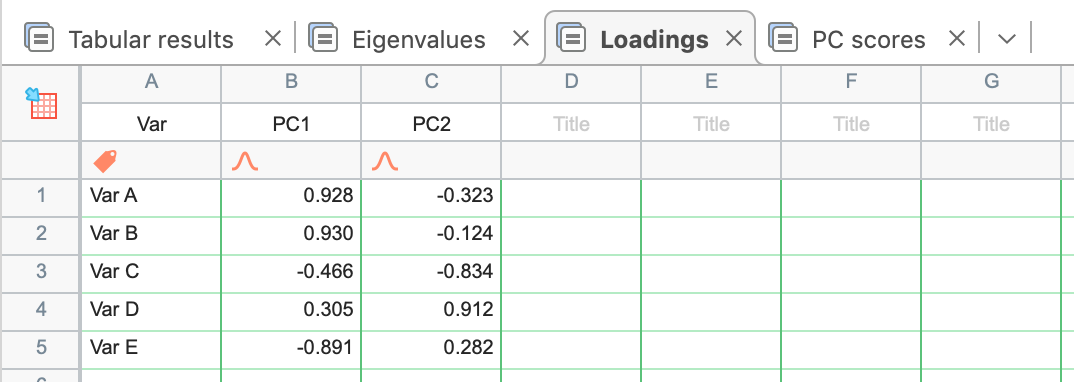
载荷还可以通过载荷图（稍后讨论）直观地显示变量间相关性的相对强度。下面是本示例数据 PCA 的载荷表和特征向量表（默认情况下不显示）。

载荷

特征向量