PCA with Prism 默认显示的最后一个选项卡是 PC 分数选项卡。在研究特征值和特征向量时，我们已经简要讨论过每个主成分的 "分数 "概念。如前所述，PC 只是数据集中变量的线性组合，这些线性组合的系数由 PC 的特征向量给出。在本示例中，请考虑 PC1。该分量的变量线性组合（使用 PC1 的特征向量值）为

PC1=0.552*（变异性 A）+0.553*（变异性 B）-0.227*（变异性 C）+0.181*（变异性 D）-0.530*（变异性 E）

要计算 PC1 的 "分数"，我们只需将标准化（或居中）数据中的数值输入该等式。每一行数据对应每个 PC 的一个 "分数"。本示例中第一行标准化数据为

 

因此，要计算 PC1 的第一项得分，可采用以下公式

PC1 = 0.552*(-1.608) + 0.553*(-1.615) - 0.227*(-0.907) + 0.181*(1.577) - 0.530*(1.392) = -1.981

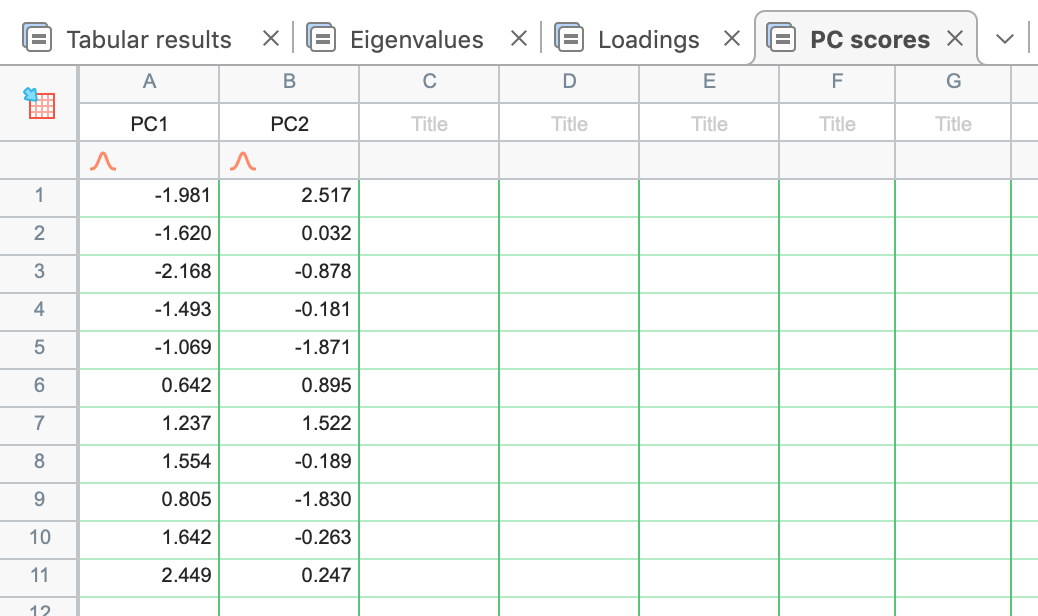
PC1 的其余分数和所有其他选定成分的分数可以用同样的方法计算，从而得出 Prism 提供的 PC 分数表：

PC 分数结果表

 

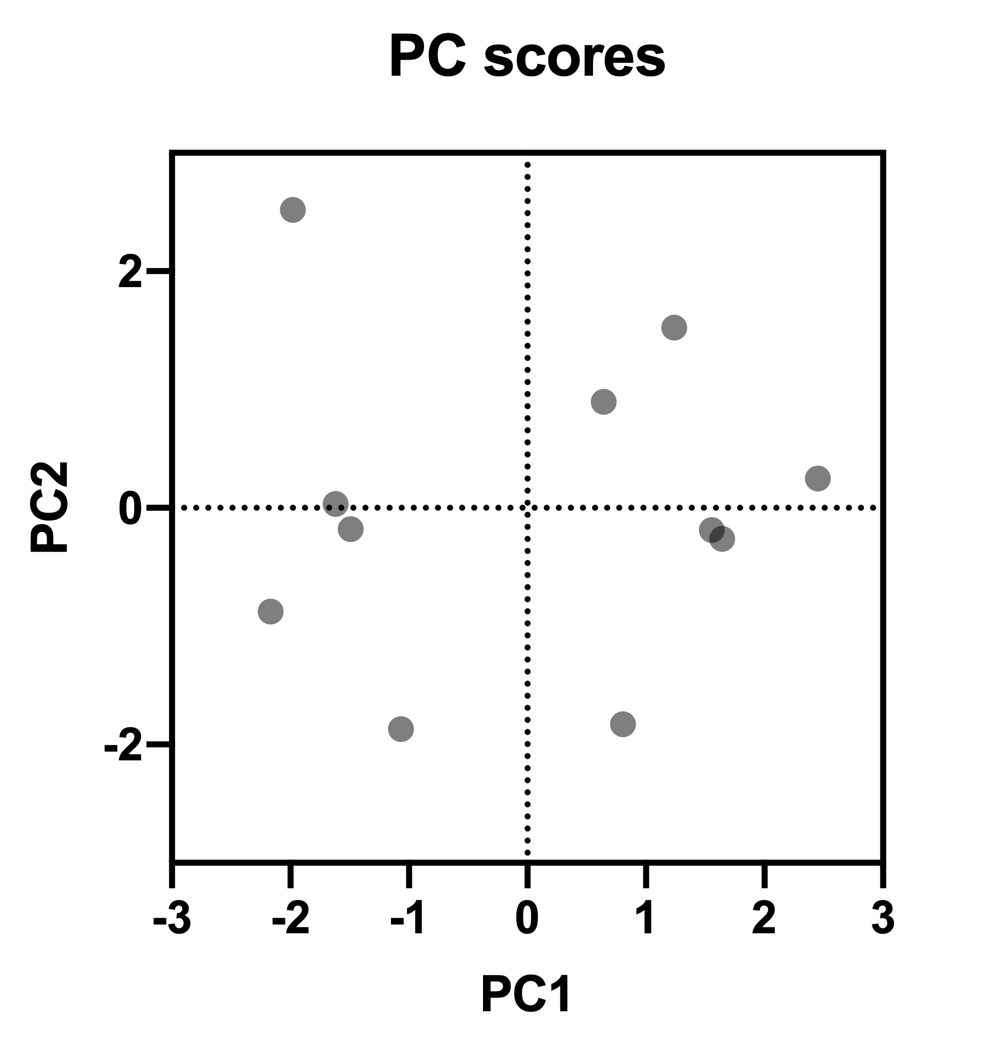
随后，这些分数可用于创建分析的 "分数图"。这些图将在不同章节中详细介绍，但总体思路是，这些分数图可以将原始数据投影到由两个选定主成分定义的二维空间中。这非常直观地体现了 PCA 的降维目标。

PC 分数图（PC1 vs PC2）