查找"特征值"或"特征向量"的严格定义不太可能得到关于这些值代表什么的合理解释，除非你深入研究计算这些值所需的矩阵代数。相反，让我们回到数据的可视化表示以及为其确定的第一个主成分：

 

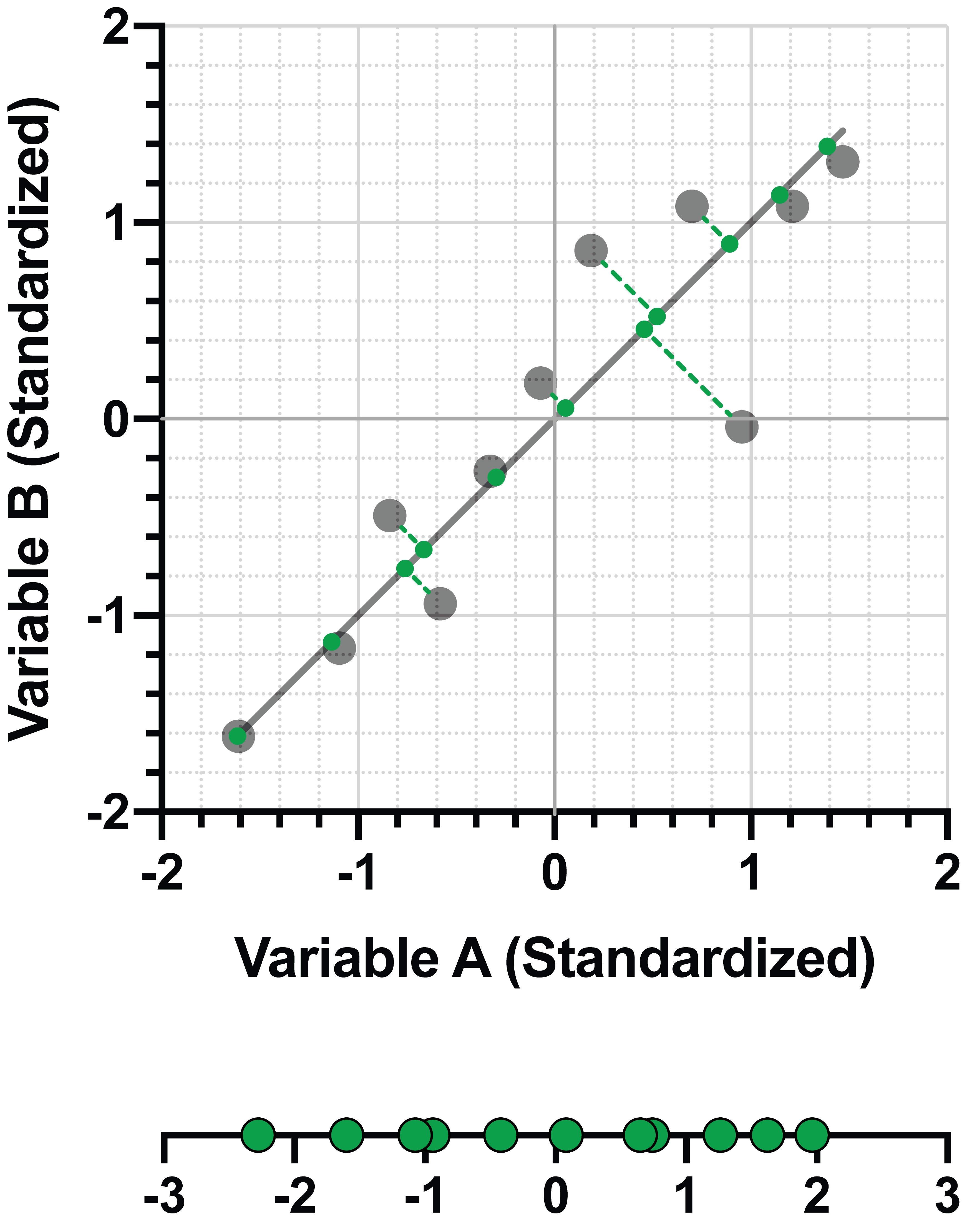
该主成分为线性组合

PC1 = 0.707*（变异性 A）+ 0.707*（变异性 B）

变量 A 的系数为 0.707，变量 B 的系数为 0.707，这两个系数共同代表了 PC1 的特征向量。简单地说，这些值代表了第一主成分的"方向"，就像斜率表示回归线的方向一样。从上图中的坐标（0,0）开始，可以看出直线的"方向"是在变异性 A 轴上向右移动 0.707，在变异性 B 轴上向上移动 0.707。这两点之间的直线就是 PC1。

高级说明：特征向量（与所有向量一样）既有方向，也有大小（如长度）。二维空间中矢量的方向可以用两个值来定义，即矢量在一维方向上的分量和矢量在二维方向上的分量。维度越多，向量就需要更多的值来全面描述。在 PCA 中，单个特征向量将为每个原始变量提供一个值。

为什么特征向量最终会出现这些奇怪的十进制值，而不是像 1 和 1 这样的简单值呢？这就要归结到勾股定理了。在前面的本示例中，我们已经证明 PC1 是通过坐标 (0,0) 和来自特征向量的坐标 (0.707, 0.707) 的直线。如果我们要确定连接这两点的直线长度（也称为矢量的大小），就会发现它等于 1！

d = √[(0.707-0)2+(0.707-0)2]=1

*注意，0.707 是一个四舍五入的值，所以上式的误差只有一点点

事实上，PC 的所有特征向量都具有这一特性。特征向量的长度总是 1，这一点可以通过求特征向量值的平方和来验证。让我们看看上述相同数据的 PC2：

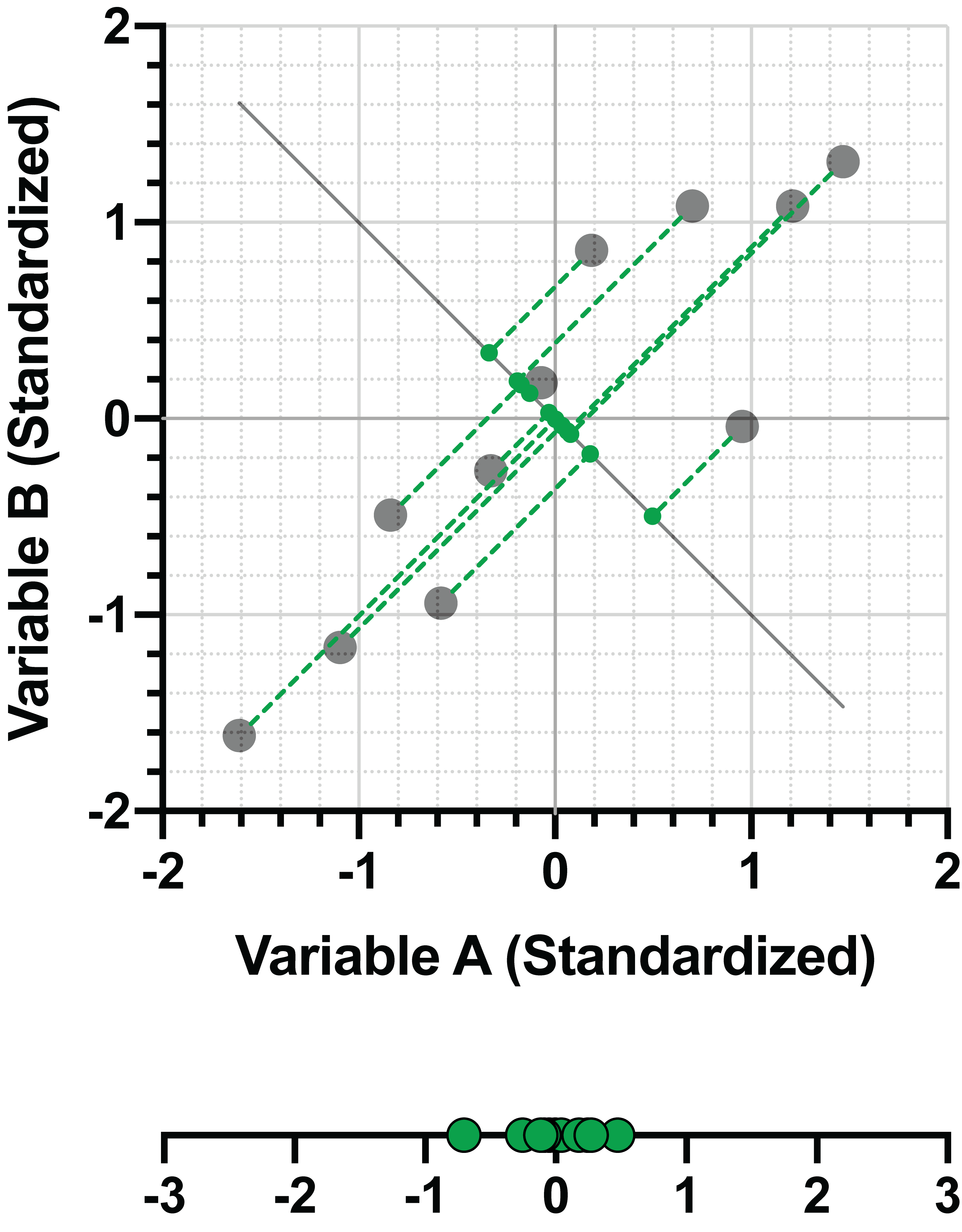
PC2 = -0.707*（变异性 A）+ 0.707*（变异性 B）

再看

d = √[(-0.707)2+(0.707)2]=1

因此，特征向量表示每个主成分的方向。那么特征值呢？原来，这些值代表了主成分所解释的方差量。对于为单一数据集确定的一组主成分，特征值较大的主成分比特征值较小的主成分能解释更多的方差。因此，特征值可视为 PC 的长度，与特征向量的方向相一致。请注意，在某些情况下，负载是用来描述原始变量与 PC 之间的这种关系的。本节将详细介绍负载及其与特征向量的关系。

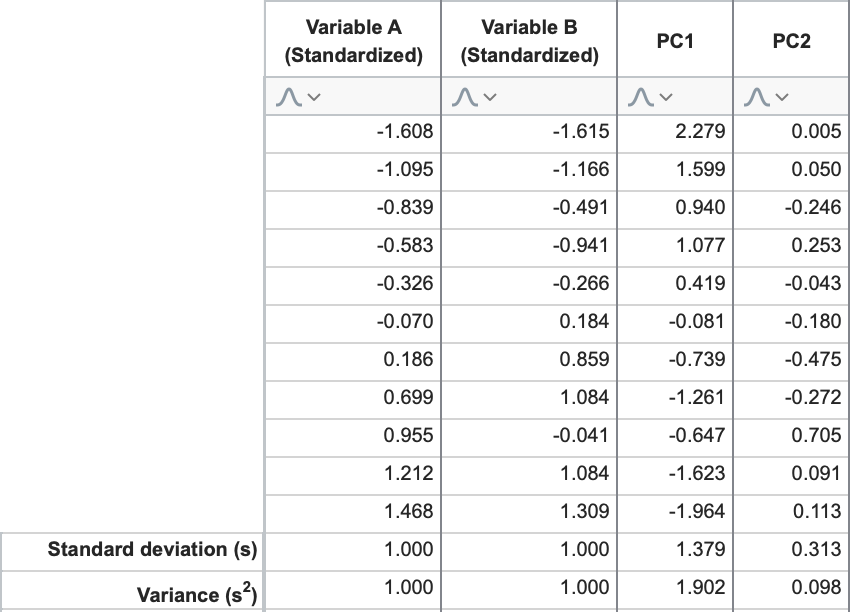
继续我们的本示例，PC1 和 PC2 的特征值分别为 1.902 和 0.098。这证实了我们之前所说的，第一个主成分解释的方差最大，而随后的每个成分解释的总方差越来越小。要直接计算这些值，请考虑我们使用线性组合和标准化数据为 PC1 和 PC2 计算的"分数"。

如果计算"PC1 分数"和"PC2 分数"两列的标准偏差，然后将这些值平方（方差 = [标准偏差]2），就会得到......你猜对了：分别为 1.902 和 0.098。

特征值之和与原始变异性的数量

在继续进行成分选择之前，还应该讨论一下特征值的另一个有趣方面。也就是说，如果使用标准化数据进行分析，所有 PC 的特征值之和将等于原始变量的总数。为什么？

请记住，标准化数据会导致每个变量的变异性等于 1。每个 PC 所"解释"的方差等于其特征值，但不会改变数据的总方差。由于将数据投影到新的 PC 上不会消除任何方差，因此所有 PC 的解释方差之和必须等于总方差。因此，特征值之和 = 解释方差之和 = 总方差 = 原始变量数。

在选择 PC 子集以实现降维时，这一事实非常有用。