如前一节所述，主成分的载荷表示变量与主成分之间的相关性（如果数据是居中而不是标准化的，载荷则表示变量与成分之间的协方差）。载荷图直观地表示了这些关系。

在我们数据的载荷图中，我们可以看到变量 A、B 和 E 与 PC1 有很强的相关性（值接近 1 或-1），而它们与 PC2 只有一定的相关性。相反，变量 C 和 D 与 PC2 的相关性很强，但与 PC1 的相关性较弱。

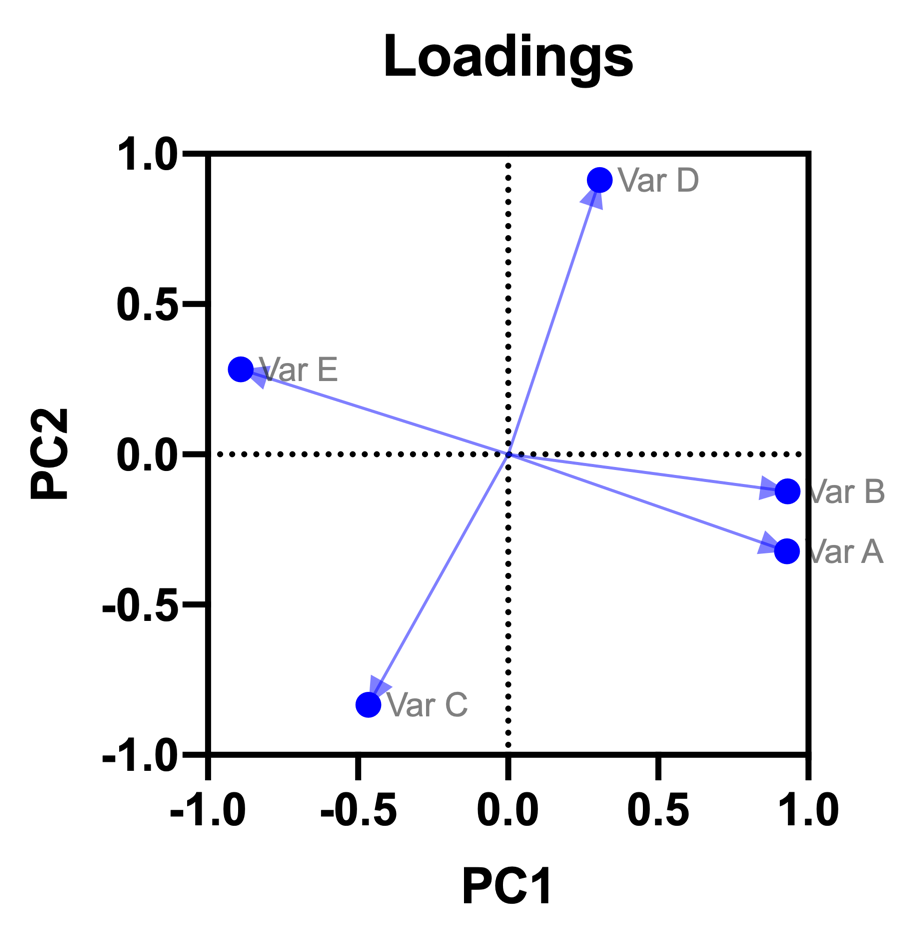
在本示例中，PC1 和 PC2 共占累计方差比例的 91.18%。在这张图上包含了如此多的信息，我们可以对各个变异性变量之间的关系有一定的了解。如上图所示，变量 A 和 B 紧紧聚在一起，表明这两个变量呈正相关。相比之下，变量 A 和 E 的向量形成了近 180°的夹角，表明这两个变量呈负相关。最后，变量 A 和 D 的向量几乎成直角，表明这两个变量可能不相关。回到原始数据的图形矩阵，我们可以确认这些假设基本正确。