PCA 的主要对象是降维。这里的变异性简单地说就是描述数据所需的变量数量。因此，简单地说，降维只是减少描述数据所需的变量数量的一种手段。

我们为什么要降低数据的维度？

在处理大型数据集时，直观地检查数据以发现数据中的趋势或模式通常很有用。这些模式可用于对观察结果进行聚类或分组，或用于了解数据中不同变异性之间的关系。请看下面的数据集：

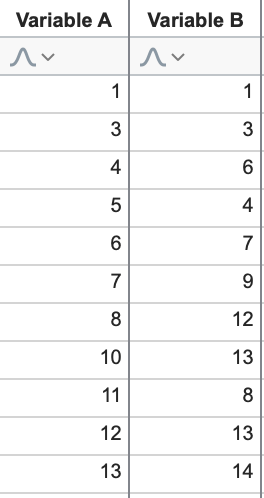
我们不难发现，一般来说，随着变异性 A 的增加，变异性 B 也会增加（正相关）。利用这些数据，我们可以快速绘制 XY 图，直观地显示这种关系。当然，看到这种关系很容易，因为只有两个变量！

但随着数据中变量数量的增加，识别数据的基本模式就变得更加困难了。请看下面的扩展数据：

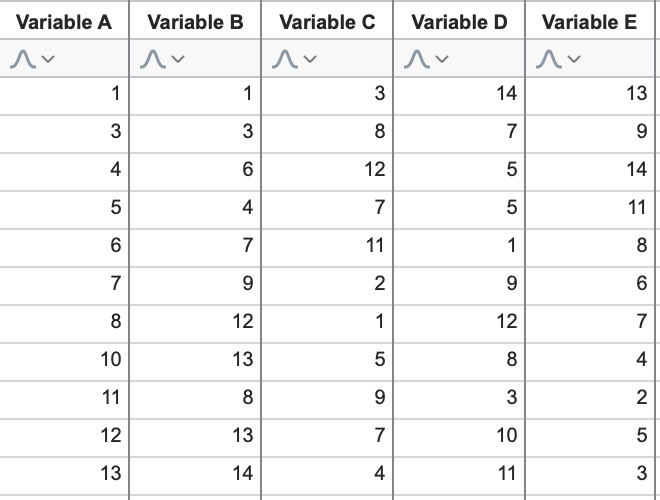
如果不绘制数据图，就不再容易发现其中的关系。使用前三个变异性变量，我们可以绘制出这样的图表，其中颜色由变量 C 的值决定：

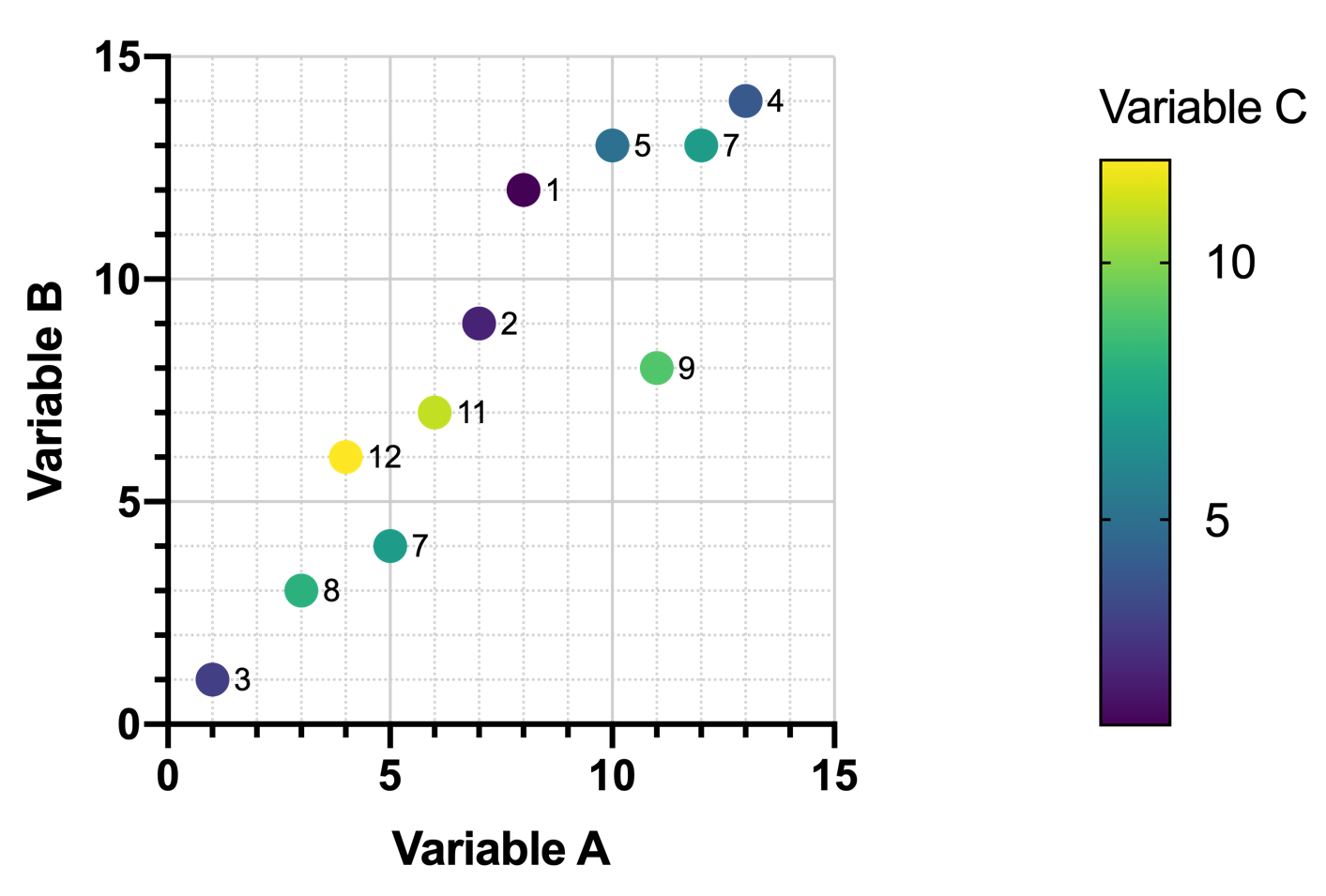
然而，即使绘制了这张图，变量 A 和变量 C（以及变量 B 和变量 C）之间的任何关系也并不明显。随着变量 A（或变量 B）值的增加，变量 C 的值似乎没有任何可预测的模式。

可以在此图中增加一个变异性变量，用其值来确定符号大小。然而，随着数据行数的增加，这类图表会变得更加难以阅读，其中的关系当然也不会让人眼前一亮。

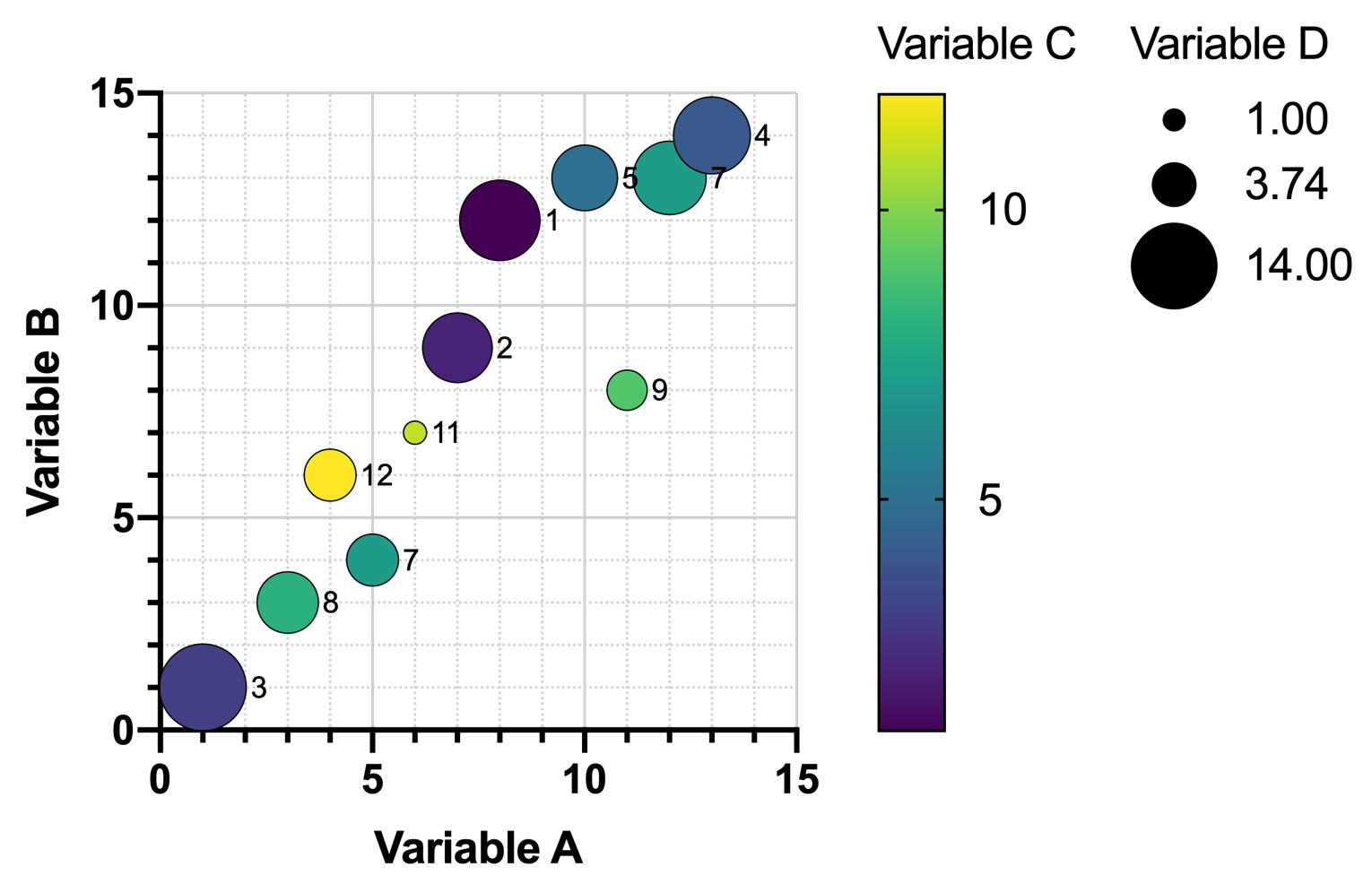
如果数据集包含大量变异性变量，则几乎不可能在一张图表上表示所有变量。可以使用图形矩阵来显示每对变量之间的关系（见下文），但这些矩阵对于同时涉及多个变量的更大的潜在关系提供的洞察力非常有限。

同时可视化多对变量的另一种方法可能是使用带有额外垂直轴的图表（本示例图表为 "三维 "图表，其中第三个垂直轴代表第三个变量或第三个维度）。然而，这些图形有其固有的局限性。最明显的限制是我们（人类）只能感知三个空间维度（高度、宽度和深度）。没有一种好的方法能以任何直观的方式同时包含三个以上的坐标轴。因此，这种解决方案不适用于具有大量变异性的数据集。

在处理具有大量变异性的数据集时，还会出现其他（非视觉）问题。最大的问题之一就是 "过度拟合"。这里我们就不细说了，简而言之就是变量变异性太大（即维度太多），我们生成的任何描述观察数据的模型都会拟合得太好，对预测未来观察值没有用。

出于这些原因，人们开发出了在不完全消除变量的情况下减少数据集维数的技术。PCA 就是其中的一种技术，它在很大程度上依赖于特征提取的概念（通过线性组合将数据投影到更少的维数上），这将在下一节中讨论。