Prism 为多重 t 检验（和非参数检验）分析提供了许多重要选项，允许您从众多不同检验中选择一种，对数据表的每一行进行检验。

实验设计选项卡

"参数"的第一个选项卡：多重 t 检验（和非参数检验）分析对话框的第一个选项卡显示了许多选项，您可以通过回答三个问题来指定要执行的分析类型：

1.数据是配对数据还是非配对数据？

2.检验是假设数据是从正态（高斯）分布、对数正态分布采样，还是不假设分布（非参数）？

3.(对数正态分布和对数正态分布的假设）：检验是否要假设等方差（标准偏差或几何标准偏差）？

4.根据前两个问题的答案，Prism 应进行哪种特异性检验？

实验设计：数据是配对数据还是非配对数据？

第一个问题涉及每个主要比较组内数据的关系。如果选择了 "配对 "选项，这意味着每个主列的第一个子列中的数据是配对或匹配的，每个主列的第二个子列中的数据是配对或匹配的，以此类推。选择本选项的本示例包括

•在不同时间对同一受试者进行的测量（本示例为治疗前后的测量）

•对根据年龄、种族或疾病严重程度等特征招募或匹配成对的个体进行测量。在这种情况下，一个人可能接受一种治疗，而另一个人则接受另一种治疗（或作为对照）。

•多次进行实验室实验，每次平行处理对照组和治疗组。如果不同制剂之间的不可控实验条件略有不同，这一点可能很重要

•测量具有某种固有配对关系的个体的变异性，如双胞胎或子女/父母配对。

请注意，配对应由实验设计决定，而绝对不应基于所分析的变异性。本示例中，如果您要比较两组人的血压测量值，根据年龄或体重匹配个体是可以的，但根据记录的血压进行匹配则是不可以的。

分布假设

许多统计分析都对所分析数据的抽样人群有一定的假设。测试中常见的假设之一就与数据采样人群的分布有关。Prism 提供了三种选择：

1.正态分布（高斯分布）--假设从正态分布中取样。比较各组平均值

2.对数正态性 - 假设从对数正态分布中取样。比较各组的几何均值

3.非参数--不假设数据是从特异性分布中采样的。相反，使用非参数检验。这通常等同于比较组内数据的等级

非参数检验并不基于数据是从高斯分布（或任何其他特异性分布）中采样的假设。这可能会让它们看起来更受欢迎。然而，非参数检验的检验力较低。决定何时使用非参数检验并不简单。

为每一行选择检验

根据前两节中选择的选项，在分析参数对话框的 "实验设计 "选项卡上最终决定执行哪 个特异性检验。每一行总共可以进行七项测试，其中有些测试还需要考虑其他选项。下面将对每个检验和最后一节中的可用选项进行说明。

1.非配对、正态（高斯）分布。在前两节中选择这种选项组合，结果是对分析中各组的标准偏差做出一个最终决定。

o第一种选择不对任何行或列中的数据所取样的群体的标准偏差做任何假设。选择该选项后，Prism 将执行不等方差非配对 t 检验（有时也称为韦尔奇校正非配对 t 检验）。对于从正态分布中采样的非配对数据，这可能是您的默认选择。

o下一个选择是假设--对于每一行--两组数据都是从具有相同标准偏差的群体中抽取的（换句话说，第一列中某一行数据所抽取的群体的标准偏差与第二列中同一行数据所抽取的群体的标准偏差相同）。这将对每一行进行标准的非配对 t 检验，并为每一行估计个别方差。

o本节的最后一个选项允许假设所有数据（所有行上的所有组）都是从具有相同标准偏差的群体中抽取的。请注意，这并不意味着您的样本标准偏差必须相同。相反，这里的假设是样本的变化是随机抽样的，所有行的所有数据都来自具有相同标准偏差的群体。这就是同方差假设，会带来更多的自由度，从而提高检验力。使用该选项后，Prism 将使用单一集合方差执行非配对 t 检验

2.配对，正态（高斯）分布。 在前两节中选择此选项组合，Prism 将只提供单一检验：

o配对 t 检验。该检验的零假设是：每对样本间差异的平均值为零

3.非配对，对数正态分布。在前两节中选择这种选项组合的结果是对分析中每组的标准偏差做出一个最终决定。

o第一种选择不对任何行或列中的数据所取样的群体的几何标准偏差做任何假设。选择该选项后，Prism 将对每一行进行韦尔奇校正的对数正态性 t 检验。对于从对数正态性分布中采样的非配对数据，这可能是您的默认选择。

o下一个选择是假设--对于每一行--两组数据都是从具有相同几何标准差的群体中抽取的（换句话说，第一列中某一行数据所抽取的群体的几何标准差与第二列中同一行数据所抽取的群体的几何标准差相同）。请注意，这一假设等同于假设对数变换后的群体方差相等。这将对每一行进行标准的对数正态性 t 检验 。

o本节的最后一个选择允许假设所有数据（所有行上的所有组）都是从具有相同几何标准偏差的群体中采样的。请注意，这并不意味着您的样本几何标准偏差必须相同。相反，这里的假设是样本的变化是随机抽样，所有行的所有数据都来自具有相同形状参数（几何标准偏差）的群体。这就是同方差假设，会产生更多的自由度，从而获得更大的检验力。使用该选项后，Prism 将以单一集合方差进行非配对 t 检验

4.配对，对数正态分布。在前两节中选择此选项组合，Prism 将只提供单一检验：

o比率 t 检验。该检验的零假设稍显复杂。简而言之，该检验的零假设是：每对比率的对数平均值为零（或者换句话说，每对比率为 1，因为 log(1) = 0）。

5.非配对、非参数检验。选择该选项组合，就必须在两种检验中选择一种：

o曼-惠特尼检验。这种检验的零假设可能很难理解，在此进行讨论。不过，需要注意的是，该检验的工作原理是：从被比较的两组中获取所有数据，并将所有这些值从小到大排序（无论该值属于两组中的哪一组）。然后，给每个值分配一个等级，最低值从 1 开始，最大值从n开始（n 是 值的总数）。然后，检验比较两组的平均等级。

oKolmogorov-Smirnov 检验。该检验的零假设可能很难理解，但假设被比较的两组是从具有相同分布的群体中抽样的。该检验使用数据的累积分布来检验是否存在违反该零假设的情况（中位数不同、方差不同或分布不同）。有关Kolmogorov-Smirnov 检验的更多信息

6.配对非参数检验。选择该选项组合后，只有一种可能的检验：

oWilcoxon配对符号秩检验。这种非参数检验首先计算被分析的两组配对之间的差异，给这些差异的绝对值分配秩和，然后比较第一组配对值较高的秩和与第二组配对值较高的秩和。这种检验理解起来比较复杂， 本指南的其他页面提供了更多关于解读这种检验结果的信息。

多重比较选项卡

在同时进行大量 t 检验时，我们的目标通常是得出一个比较子集，其中的差异似乎足够大，值得进一步研究。在多重比较检验（和非参数）分析之后，Prism 提供了两种方法来确定双尾 P 值是否足够小，从而使该比较值得进一步研究。

一种方法是基于我们熟悉的统计学显著性思想。

另一种选择是根据错误发现率（FDR；推荐）来决定。 控制 FDR 的整个思路与宣布某些比较具有 "统计学显著性"完全不同。 这种方法不使用 "显著"一词，而是使用 "发现"一词。 您设定的 Q 值是所期望的 "发现"中错误发现的最大百分比。换句话说，它是所需的最大 FDR。

在所有标记为 "发现 "的数据行中，目标是不超过 Q% 的数据行是错误发现（由于数据的随机散布），而至少 100%-Q% 的发现是群体均值之间的真实差异。了解有关 FDR 的更多信息。Prism 提供三种控制 FDR 的方法。

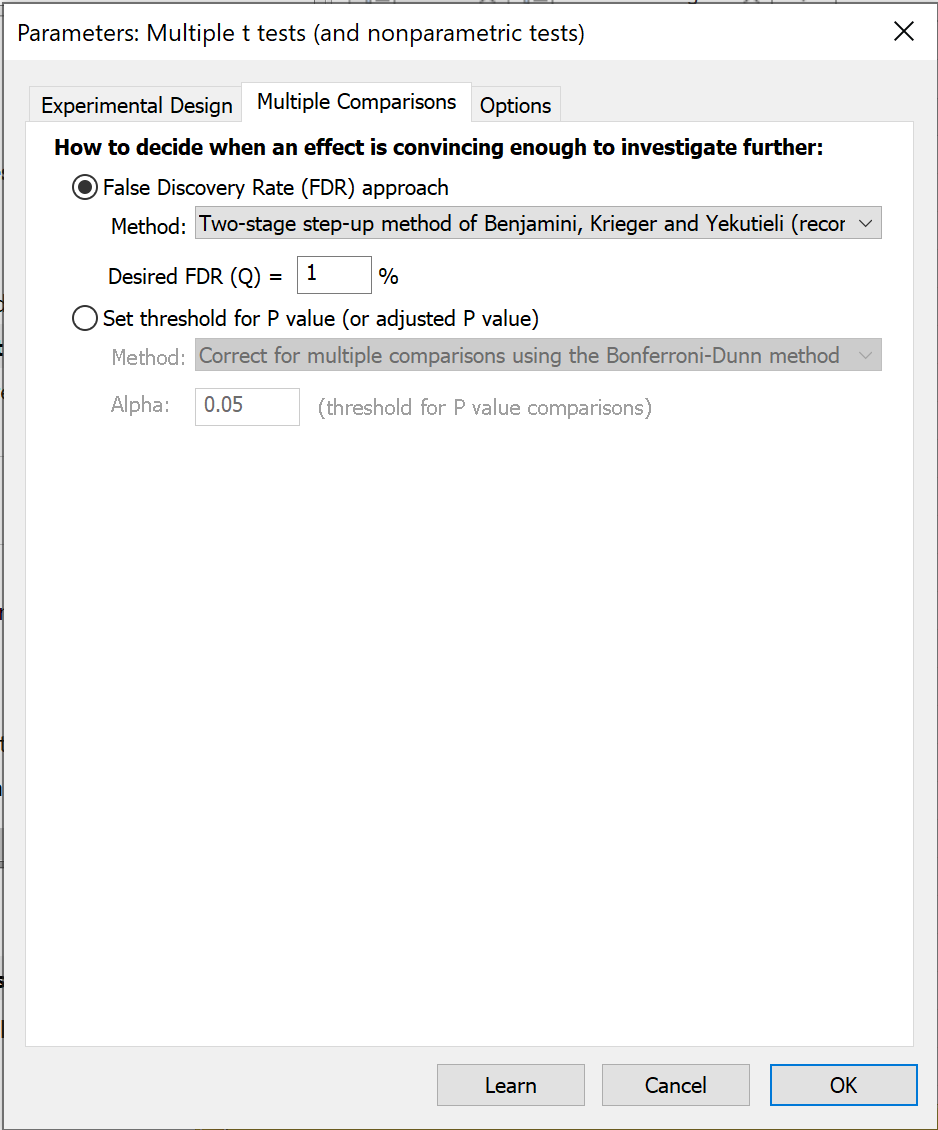
如何处理多重比较

如果选择错误发现率方法，则需要选择 Q 值，即可接受的错误发现率百分比。请输入百分比，而不是分数。如果您愿意接受 5%的假阳性发现，请输入 5 而不是 0.05。您还需要选择使用哪种方法。

如果您选择使用统计学显著性方法，则需要对多重比较做出额外的决定。您有四种选择：

•使用Holm-Šídák 方法修正多重比较（推荐）。 您可以指定要用于整个 P 值比较族的阈值水平 alpha。这种方法的设计原理是，指定的 alpha 值代表的是，如果零假设实际为真，那么在每一行的比较中，一个或多个比较获得 "显著 "P 值的概率。

•使用 Šídák-Bonferroni 方法修正多重比较（不推荐）。我们建议使用 Holm-Šídák 方法（见上文），该方法检验力更强。Šídák-Bonferroni方法，通常只称为Šídák方法，比普通的Bonferroni-Dunn方法（通常只称为Bonferroni方法）更有检验力。这在进行多次比较时尤其如此。

•使用 Bonferroni-Dunn 方法修正多重比较（不推荐）。与 Holm-Šídák 方法相比，Bonferroni-Dunn 方法更容易理解，也更广为人知，但它没有其他优点。Bonferroni-Dunn 法和Šídák-Bonferroni法的主要区别在于，Šídák-Bonferroni 法假定每项比较都是独立于其他比较的，而 Bonferroni-Dunn 法则没有这种独立性假定。因此，Šídák-Bonferroni 检验力略高于 Bonferroni-Dunn 检验力。

•不进行多重比较校正（不推荐）。每个 P 值都单独解读，不考虑其他 P 值。为显著性水平设置一个值，即 alpha，通常设置为 0.05。该值是比较 P 值的临界值。如果 P 值小于 alpha，则认为该比较具有 "统计学显著性"。如果使用这种方法，要知道你会得到很多假阳性（你会得到很多 "有意义 "的发现，但事实证明并非如此）。在某些情况下，比如药物筛查，多重 t 检验的结果只是用来设计下一阶段的实验，这并无大碍。

选项选项卡

参数 "中的第三个也是最后一个选项卡：多重 t 检验（和非参数检验）分析对话框中的第三个也是最后一个选项卡提供了许多重要的控制选项，用于设置如何报告分析结果以及 Prism 将根据分析结果生成何种可视化效果。

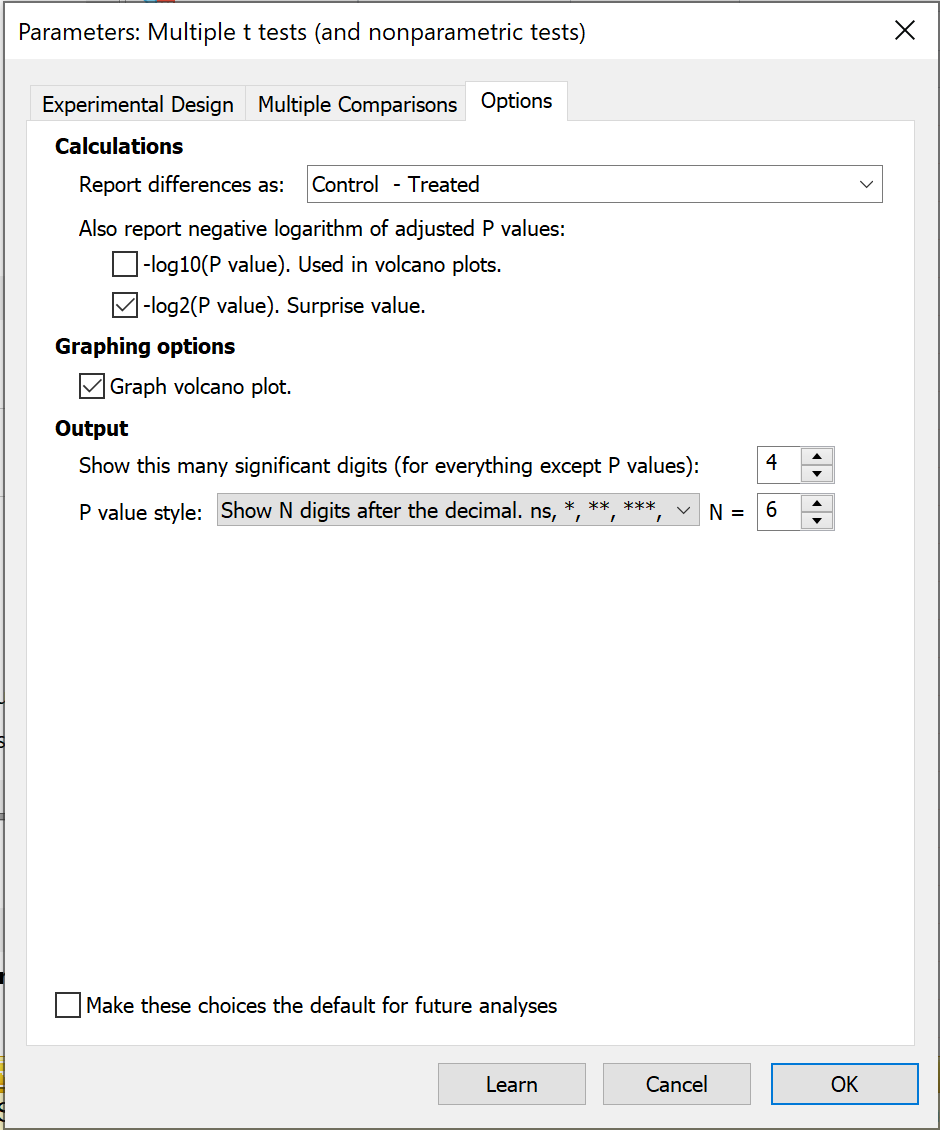
计算

在本节中，您可以选择分析中两组比较的顺序。本示例中，您可能不希望以 "对照组 - 治疗组"的形式报告差异，而是希望以 "治疗组 - 对照组"的形式报告结果。请注意，这不会改变测试的整体结果，只会改变差异的 "符号"。

在本节中，还可以选择报告计算 P 值的两种对数变换：

•log10(P值)--在绘制结果的火山图时使用这种转换，该选项可用于生成这些结果的表格（与绘制的火山图一起报告非常有用）

•-log2（P 值）--这是计算 P 值的 2 阶对数，有时也被称为 "香农信息值"、"惊喜值"或 "S 值"。计算出的 P 值的这种简单变换提供了一种直观的 P 值思维方式。应用这种变换得到的值 S 可以这样解读：我们对得到的 P 值的惊讶程度不应该超过掷硬币 S 次而每次都是人头的惊讶程度。本示例中，假设 P 值为 0.125。相应的 S 值将是 3，我们得到 0.125 的 P 值不会比掷三次硬币三次都是人头更令人惊讶（不会太 令人惊讶）。假设 P 值为 0.002。相应的 S 值为 ~9，我们对 P 值为 0.002 的结果不会比掷9次硬币而每次都是人头更惊讶（更惊讶！）。

图表选项

这里的复选框（默认启用）会使 Prism 绘制数据的火山图。X 轴是每行平均值之间的差值。Y 轴绘制 P 值的转换图。特异性地，它绘制 P 值的负对数。因此，如果 P=0.01，log(P)=-2，-log(P)=2，这就是绘制的结果。因此，差值较大的行会更靠近图表的任一边缘，而 P 值较小的行会绘制在图表的较高位置。

Prism 会自动在 X=0 处放置一条垂直网格线（无差异），并在 Y=-log(alpha) 处放置一条水平网格线。该水平网格线上方的点的 P 值小于您选择的 alpha 值。

输出

最后，在这个选项卡上，您可以控制分析结果中显示多少位有效数字（P 值除外），以及报告 P 值时使用的样式。