Prism 提供三种控制 FDR 的算法供选择。这三种算法的工作方式类似。
1.计算每个比较的 P 值。
2.将 P 值从低到高排序。
3.从最大 P 值开始。
4.计算最大 P 值的阈值。该阈值依赖于 P 值的数量。 对于 Benjamini、Krieger 和 Yekutieli 的方法,阈值还依赖于该方法提供的真零假设数量的估计值。
5.如果 P 值小于阈值,那么所有的 P 值都会被标记为发现,这样就完成了。否则,继续。
6.转到第二大 P 值。
7.计算第二大 P 值的阈值。该阈值将小于最大 P 值的阈值。计算临界值(见下文)依赖于 P 值的等级、P 值的数量以及(对于 Benjamini、Krieger 和 Yekutieli 的方法而言)真零假设数量的估计值(由该方法计算得出;无需您思考)。
8.如果 P 值小于阈值,则该 P 值和所有更小的 P 值都会被标记为发现,然后就完成了。 否则继续。
9.转到下一个 P 小值。
10.为这个等级计算一个阈值。它将小于前一个阈值。
11.如果 P 值小于阈值,则将该 P 值和所有更小的 P 值标记为发现,完成。 否则,重复步骤 9-10 直到完成。
这三种方法的区别在于如何计算阈值。下表给出了详细信息,其中 Q 是期望的错误发现率(百分比),N 是集合中 P 值的个数,Ntrue 是估计为真的零假设个数(下面第二种方法的一部分)。定义 q 等于 Q/100。这将您输入的百分比值转换为分数。
方法 |
最小 P 值阈值 |
最大 P 值阈值 |
本杰明尼和霍赫伯格的原始方法 (1) |
q/n |
q |
Benjamini、Krieger 和 Yekutieli 的两阶段递升法 (2) |
q/[(1+q)Ntrue] [q/(1+q) Ntrue] (2) |
[q/(1+q)] * (N / Ntrue) |
Benjamini & Yekutieli 的修正方法 (3) |
q/[N* (1 + 1/2 + 1/3 +... + 1/N)] q /(1 + 1/2 + 1/3 +... + 1/N) |
q /(1 + 1/2 + 1/3 + ... + 1/N) |
注:
•变量 q 定义为 Q/100,其中 Q 是您输入的期望错误发现率(百分比)。
•介于最小值和最大值之间的 P 值的阈值由这些极端值之间的线性插值决定。
•阈值以分数(而非百分比)的形式计算,以便与 P 值进行比较。
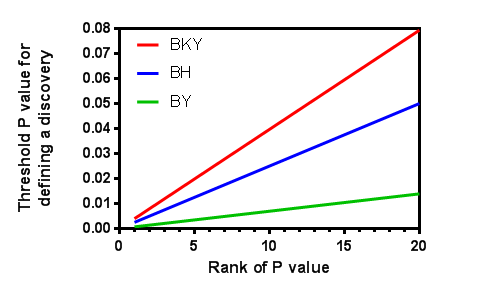
下面的图表显示了分析 20 个 P 值(N=20)的阈值,您集 Q=5% 和 Ntrue=12(由 BKY 方法根据数据计算得出,仅适用于红线)。您可以看到,Benjamini、Krieger 和 Yekuteili 的两阶段线性递升法方法(红色)的阈值最大,所以检验力最强,而 Benjamini & Yekutieli 的修正方法(绿色)检验力最小。您还可以看到,在计算最大 P 值的阈值时,这些方法的分歧最大,而在计算较小 P 值时,这些方法几乎趋于一致。
参考文献
1.Benjamini, Y. & Hochberg, Y. 《 控制错误发现率:多重检验的实用而有力的方法》。皇家统计学会杂志》。B 系列(方法论)289-300(1995 年)。
2.Benjamini, Y., Krieger, A. M. & Yekutieli, D.Adaptive linear step-up procedures that control the false discovery rate.Biometrika 93, 491-507 (2006).我们使用本文第 6 节定义的方法,即两阶段线性递升程序。
3.Benjamini, Y., & Yekutieli, D. (2001)。依赖度下多重检验中错误发现率的控制。统计年鉴》,1165-1188。