Prism 提供多种相关测试,可对三个或更多组进行比较。您对试验的选择依赖度取决于这些选择:
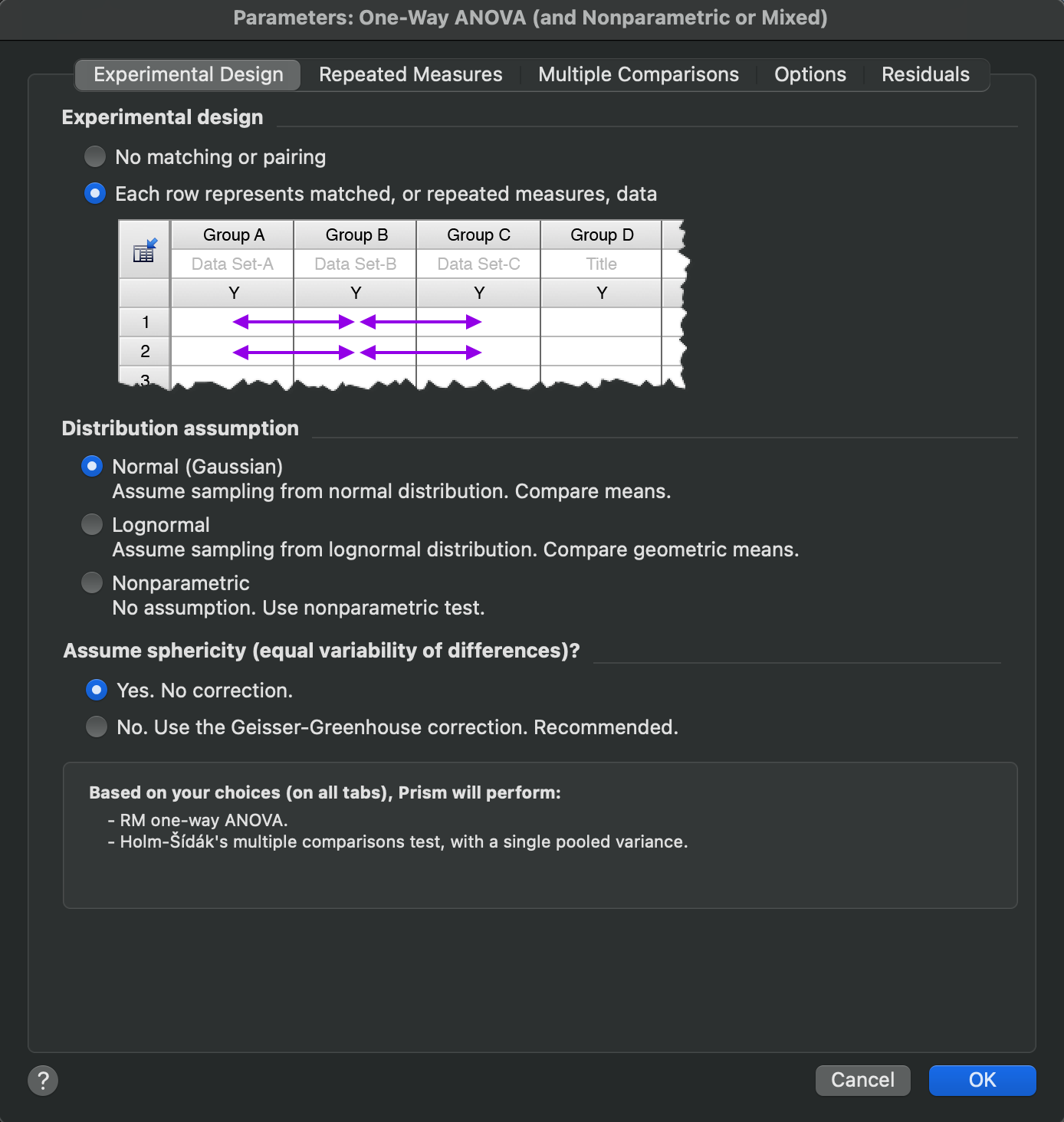
实验设计
当数据列匹配时,选择重复测量检验。下面是一些本示例:
•您对每个受试者的一个变异性进行了多次测量,可能是在干预前、干预中和干预后。
•招募受试者作为匹配组,根据年龄、种族和疾病严重程度等变量进行匹配。
•多次进行实验室实验,每次都同时进行几种处理。由于您预计实验与实验之间会有变异性,因此您希望在分析数据时将每次实验都视为匹配集。
配对不应基于所比较的变异性。如果您要比较三组人的血压,根据年龄或邮政编码匹配组是可以的,但根据血压匹配组是不可以的。
重复测量一词严格适用于对一个受试者反复进行治疗的情况(上述第一个示例)。另外两个本示例称为随机区组实验(每组受试者称为一个区组,在每个区组内随机分配治疗)。重复测量和随机区组实验的分析方法相同,Prism 总是使用重复测量一词。
如果是完全随机设计,请选择 "无匹配"。
分布假设
许多统计分析都对所分析数据的抽样群体有一定的假设。测试中常见的假设之一就与数据取样群体的分布有关。Prism 提供了三种选择:
1.正态分布(高斯分布)--假设从正态分布中取样。比较各组平均值
2.对数正态性 - 假设从对数正态分布中取样。比较各组的几何均值
3.非参数--不假设数据是从特异性分布中采样的。相反,使用非参数检验。这通常等同于比较组内数据的等级
非参数检验并不基于数据是从高斯分布(或任何其他特异性分布)中采样的假设。这可能会让它们看起来更受欢迎。但是,非参数检验的检验力较低。决定何时使用非参数检验并不简单。
如果没有匹配:假设方差相等(同方差)?
通常方差分析 F 检验的一个基本假设是方差齐性。这意味着每组平均值都是从方差相同的群体中抽样得到的。对于从正态分布中采样的数据,这意味着即使均值不同,群体的标准偏差也相同。对于从对数正态分布中采样的数据,这意味着即使几何均值不同,各群体也具有相同的几何标准偏差。
从 Prism 8 开始,您可以选择是否假设种群方差相等。如果不做假设,Prism 会执行两种不同形式的方差分析,并报告两种结果。 Welch 方差分析 和 Brown-Forsythe 方差分析都 会调整 F 比和自由度的计算,以调整组内方差的异质性。P 值的解读方式与方差分析表相同。
注释
•为什么要使用这些特殊形式的方差分析,而不是使用非参数 Kruskal-Wallis 检验呢?因为虽然 Kruskal-Wallis 检验不对数据采样的分布做任何假设,但它确实假设了分布的离散度或扩散度是相同的。
•作为这些检验值的替代方法,可以考虑对数据进行转换(倒数等),然后用普通方差分析对转换后的值进行分析。
•这种比较均值的布朗-福斯替检验不同于另一种也叫布朗-福斯替的比较方差的检验。
如果是重复测量:假设球形性?
球形性的概念
球形性的概念很难理解。简而言之,它意味着您在两次治疗之间等待的时间足够长,以消除任何治疗效应。如果您的数据不是重复测量数据,或者您选择的是非参数检验,那么这个概念就无关紧要了。
对于每个受试者,用 A 栏中的值减去 B 栏中的值,然后计算出这一系列差异的标准偏差。现在对 A 列与 C 列、B 列与 C 列之间的差异做同样的处理,等等。如果球形假设成立,那么所有这些标准偏差都应该有相似的值,任何差异都是偶然造成的。如果这些标准偏差之间存在较大的系统性差异,则球形性假设不成立。
如何决定是否假设球形性
如果每一行数据都代表一组匹配的观察结果,那么就没有理由怀疑球形性假设。这种设计有时称为随机区组实验设计。
如果每一行数据都代表一个受试者连续接受的处理,那么就属于重复测量实验设计。如果每个受试者的治疗顺序是随机的,那么球形性假设就不太可能成为问题,因为一个受试者先接受 A 治疗,然后接受 B 治疗,最后接受 C 治疗;而另一个受试者先接受 B 治疗,然后接受 A 治疗,最后接受 C 治疗......。但如果所有受试者的治疗顺序相同,最好不要假设球形性。
如果您不确定,我们建议您不要假设球形性。
您的选择对 Prism 计算的影响
如果您选择不假设球度,Prism 将
•在计算重复测量方差分析 P 值时包含 Geisser-Greenhouse 修正。由此得出的 P 值将高于未进行校正时的 P 值。
•通过报告ε来量化球形违背情况。
如果您要求 Prism 假设球形性,但事实上违背了这一假设,那么方差分析的 P 值就会过低。因此,如果您不确定是否要假设球形性,我们建议您选中不假设球形性选项。