概览

重复测量方差分析的假设之一称为球形性或圆周性（两者是同义词）。Prism 可以让您决定是否接受这一假设。如果选择不接受该假设，Prism 会使用 Geisser 和 Greenhouse 的修正方法来修正违反该假设的情况。

是否应该假设球度？

球形性的定义如下，但以下是回答 Prism 关于是否假设球形性问题的一些指导原则：

•如果您的实验设计依赖于匹配而非重复测量，那么您可以假设球形性，因为违背球形性的可能性不大。

•如果您的实验设计是重复测量（在一段时间内进行多次测量），我们建议您不要假设球形性。我们遵循麦克斯韦和德莱尼的建议(1)。

球度的定义

这个名字很容易混淆。不要试图通过球体来直观理解球度一词的含义。数学统计书籍从矩阵代数的角度来定义这个术语。这让人觉得很困惑。但事实上，这个概念非常容易理解。

下面是 Prism 中的样本数据表（选择列表，然后选择重复测量方差分析的样本数据）。

 

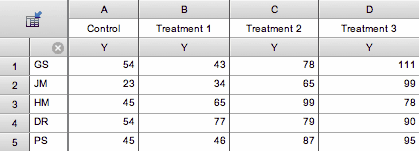
每一行代表一个受试者的数据，由行标题标识。每列代表不同的处理。在本示例中，五个受试者中的每个人都接受了四种顺序处理。数据将通过重复测量方差分析进行分析。

球形性假设指出，处理 A 和处理 B 之间差异的方差等于 A 和处理 C 之间差异的方差，等于 A 和处理 D 之间差异的方差，等于 B 和处理 D 之间差异的方差...... 像所有的统计假设一样，这个假设涉及到数据采样的人群，而不仅仅是这些特定的数据集。

在图表中更容易看出这一点：

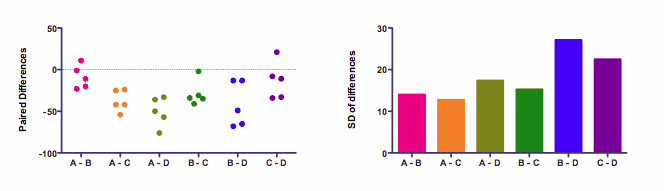
左侧面板显示的是差异。六列中的每一列都代表两种处理之间的差异。共有五个受试者，因此每个差异有五个点。

右图显示的是标准偏差。球形性假设指出，数据是从这些标准偏差相同的群体中抽样得到的。(大多数统计书都提到方差，即标准偏差的平方）。如果标准偏差相等，方差也相等）。右图中的标准偏差并不相同。这并不重要。 假设是关于数据取样的总体值。在任何特定的样本中，都会存在一些差异。在这里，标准偏差之间的差异相当小。

你可能会对考虑非相邻列之间的差异感到惊讶。为什么要考虑 A 和 C 之间的差异？或者 A 和 D 之间的差异？答案是方差分析，即使是重复测量方差分析，也不关注组的顺序。重复测量方差分析将每一行数值视为一组匹配值。但是，处理的顺序根本没有考虑在内。如果你随机打乱所有受试者的处理顺序，方差分析结果不会有丝毫改变（除非你选择趋势后检验）。

下面的参考文献 2 和 3 对球形性做了清晰的非数学解释。

复合对称性

在阅读本专题时，您还会遇到 复合对称性这一术语，它是基于原始数据的协方差矩阵（不计算配对差异）。 如果复合对称性假设对数据集有效，那么球形性假设也有效。但反过来也不总是正确的。即使球形性假设有效，数据也有可能违背复合对称性，但这种情况很少见。

球形性假设遭到违背时会发生什么？

如果重复测量的时间间隔太短，导致某个值偏高（或偏低）的随机因素在下一次测量前没有冲淡或消散，就会违背球形性假设。为避免违反该假设，在两次治疗之间要等待足够长的时间，以便受试者与治疗前基本相同。在可能的情况下，还要随机安排治疗顺序。

如果违背了球形性假设，而您又没有在计算中考虑到这一点，那么重复测量方差分析所报告的 P 值就会太小。 换句话说，Greenhouse-Geisser 修正会增加 P 值。

量化球形度偏差

Prism 通过计算和报告ε值来量化球形度偏差。

Prism 似乎应该能够根据ε值来决定是否对球形违背进行校正。但是，不建议使用该值来决定如何分析数据(1)。

不假定球形性的重复测量方差分析

Prism 可以使用 Greenhouse 和 Geisser 的方法来调整重复测量方差分析的结果，以考虑到 epsilon 的值。这种调整的唯一作用是减少自由度数，从而增加 P 值。

注：

•这种方法有时归功于 Box。

•Geisser和Greenhouse也得出了一个 下限修正法。这种方法计算比较简单，但修正的范围太大。Prism 没有使用这种方法，而是使用 Geisser 和 Greenhouse 的ε帽子法。

•Huynh 和 Feldt 开发了另一种方法，可以在不假设球形性的情况下进行重复测量方差分析。Prism 并不计算这种方法，因为 Maxwell 和 Delaney 更喜欢（稍微喜欢）Geisser 和 Greenhouse 方法 (1)。

•校正是通过降低自由度值来实现的。这些修正值可以是分数，Prism 根据 F 比值和这些修正的分数自由度计算 P。

•如果通过拟合混合模型来拟合数据，校正的作用也是一样的。模型的拟合与未要求校正时相同。自由度减小了，因此根据 F 比计算出的 P 值增大了。

在查看 Prism 结果的打印页面时，如何判断是否假设了球形性？

如果没有假定球形性，您会看到 Prism 报告了 Geisser-Greenhouse epsilon 的值，并且分数 df 值用于计算 P 值。

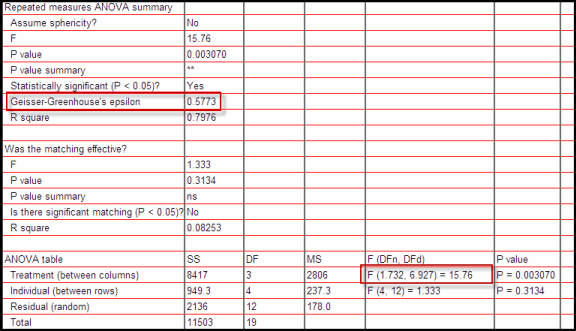
参考文献

1.Scott E. Maxwell, Harold D. Delaney, Designing Experiments and Analyzing Data：第二版。IBSN：0805837183。

2.Andy Field,A Bluffer's Guide to ...Sphericity.

3.T. Baguley,What is all this stuff about sphericity in my repeated measures ANOVA Output?