问题出在哪里？重复测量方差分析无法处理缺失值

重复测量方差分析计算需要完整的数据。如果某个参与者或动物的值缺失，就需要忽略该参与者或动物的所有数据。 克服这一问题的唯一方法（使用方差分析）是估算缺失值的可能值，然后在没有任何缺失值的情况下进行分析，修正结果（减少 df）以考虑到估算。这不是首选方法，Prism 也不提供这种方法。

Prism 提供拟合混合效应模型来分析缺失值的重复测量数据。

拟合混合效应模型--全貌

混合效应模型方法非常通用，可用于分析各种实验设计。有关混合效应模型的书籍很多。 由于这种通用性，混合效应模型方法（一般来说）并不适合初学者。

也就是说，Prism 能够对重复测量数据拟合混合效应模型。Prism 使用混合效应模型方法，如果没有缺失值，结果与重复测量方差分析相同；如果有缺失值，结果也相当。这里有一个例外，即如果混合效应模型中随机效应的方差为零或负值。在这种情况下，混合效应模型和重复测量方差分析的结果会有所不同。

Prism 仅在这一种情况下使用混合效应模型。 您不必也不可能定义协方差矩阵。不能添加协方差。不能比较其他混合效应模型。不能进行混合效应模型回归。

在 Prism 中拟合混合效应模型时，可以将其视为允许缺失值的重复测量方差分析。

混合效应？固定因素与随机因素

统计计算可以处理两种因素。

•当您希望检验已收集数据的特定组平均值之间的差异时，一个因素是固定的。

•当您从无限（或至少大量）可能的群体中随机选择群体，并且您希望就所有群体（而不仅仅是您从中收集数据的群体）之间的差异得出结论时，该因素就是随机因素。

方差分析的原理是将数值之间的总变异分为不同的部分。在重复测量方差分析中，其中一个组成部分就是参与者或组块之间的差异。在 Prism 中，方差分析将包括参与者或组块在内的所有因素都视为固定因素。

顾名思义，混合效应模型法是根据数据拟合一个模型。模型之所以是混合模型，是因为其中既有固定因素，也有随机因素。当 Prism 对重复测量数据进行混合模型分析时，它会假定主要因素（在单因子中由数据集列定义，在双因子和三因子中由数据集列和行定义）是固定的，但受试者（或参与者，或运行......）是随机的。您对这些特定参与者之间的变异不感兴趣，但想知道参与者之间的总体变异。

两种方法的结果

重复测量方差分析和拟合混合效应模型的结果看起来很不一样。下面是两种方法分析单向重复测量数据（无缺失值）的本示例。

重复测量方差分析结果

 

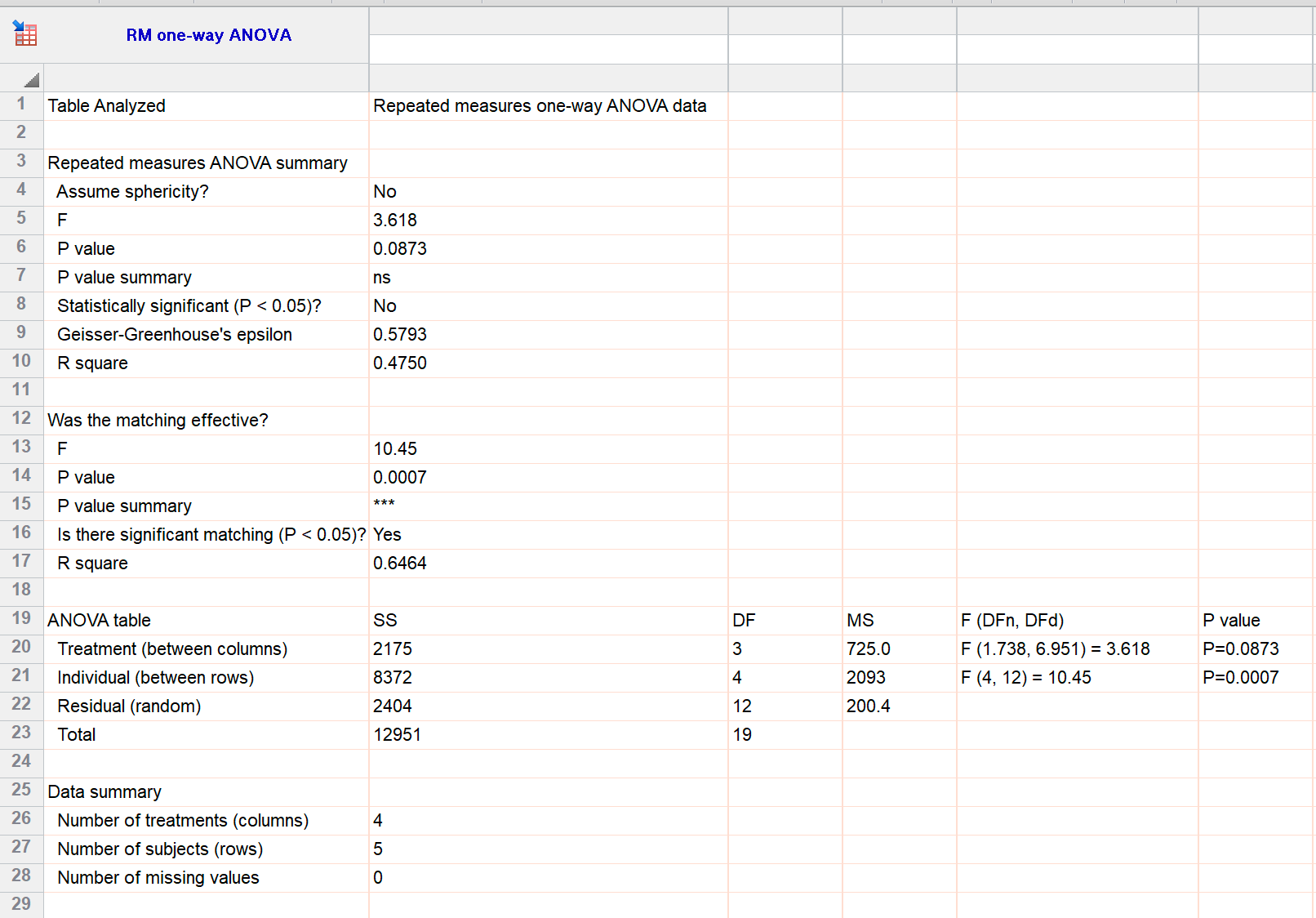
混合效应模型结果

主要结果相同

主要结果是检验所有处理组具有相同组平均值这一零假设的 P 值。两种方法的该 P 值均为 0.0873（方差分析为第 6 行，并在第 20 行重复；混合效应模型为第 6 行）。对于这些数据，处理之间的差异在统计学上并不显著。

多重比较结果相同

重复测量方差分析后的多重比较由集合标准偏差计算得出，标准偏差是均方残差的平方根。

拟合混合效应模型后的多重比较要复杂得多，它基于矩阵代数。在没有缺失数据的情况下，两者是等价的。

部分结果不同

一部分结果不同，即检验受试者之间是否确实存在变异的部分。方差分析通过将受试者之间的变异作为变异成分之一来检验这一点，并用 F 比和 P 值检验其贡献，其结果为 0.0007（上文第 21 行）。 混合效应模型比较了受试者是随机因素的模型与忽略受试者之间差异的模型的拟合程度。其结果是卡方检验比率和 P 值均为 0.0016（上文第 14 行）。 由于固定效应方差分析假设受试者是一个固定因素（您关心的是那些特异性受试者），而混合效应模型将受试者视为一个随机因素（您关心的是一般受试者），因此这两个 P 值通常不一样。