Cox 比例风险回归的目的是生成一个人群中发生特定事件的风险率模型。这个人群是由各种不同的预测因子变量定义的，模型中使用这些变量来估计这个危险率。根据这一危险率，可以估算出所研究人群的生存函数。在进行 Cox 比例风险回归时会有许多假设，您在进行这种分析时应该了解这些假设。在本页中，您会发现在进行 Cox 比例风险回归或解读该分析结果时需要注意的一些重要问题。
各组的风险函数是否成比例？
考虑到本分析的名称，首先询问比例风险假设是否成立才有意义。这一假设主要是指，有且仅有一个基本的基线危险函数适用于整个观察群体。任何给定个体（或群体）的危险率都是这一基线危险函数的缩放版本。应用于该基线危害函数的缩放量基于模型中针对该个体（或群体）的预测因子的值。如果比例风险假设成立，那么一个人在一个时间点的风险是基线风险的 3 倍，那么他在所有 时间点的风险都是基线风险的 3 倍。这也意味着，任何两个个体或组别之间的风险比在任何时候都必须保持不变。如果男性的风险比与女性的风险比为 2.5，这就意味着男性在任何时候发生相关事件的风险都是女性的 2.5 倍。这是一个相当大的假设，考虑到生物系统的复杂性和变异性，这个假设可能并不总是完全正确的。要检验这一假设，可以创建对数减对数图（使用 Prism 中 Cox 回归参数对话框的残差选项卡创建这些图）。
如果违反了比例风险假设，可以使用一些方法来尝试说明这一点。一种常见的方法是使用违反 PH 假设的变异性对模型进行分层。一旦确定，就会根据该变量的水平将输入数据分成新的组别。之后，对每个新的组别分别拟合 Cox 比例风险回归模型。这一过程有时被称为拟合 "分层 Cox 模型"。不过，Prism 并不提供自动执行此操作的选项。
数据组织是否正确？
为了在 Prism 中执行 Cox 比例风险回归，必须将数据输入多变量数据表。对于该表，每列是一个变异性，每行是一个观测值。必须为每个观察值（行）输入一个值：
•事件（响应）变异性时间
•事件/删剪（结果）指标变量
•模型中的每个预测因子变量
如果某行缺失任何一个变量的值，则在拟合模型时将省略该行。请注意，缺失事件/监控变量值的观察值（行）将不 用于拟合模型，但在拟合模型后仍可使用参数对话框的预测选项卡计算估计生存概率（如果为该观察值提供了事件发生时间变量值）。
我的 Cox 比例风险回归模型应该有截距项吗？
不！与多元线性回归不同，Cox 比例风险回归没有截距项。这里没有显示数学上的理由，但一般的解释是--由于基线危险（h0(t)）是未定义的，任何添加到模型中的常数截距项都会被 "吸收 "到基线危险中。因此，在定义 Cox 比例风险回归模型时，不需要（或不允许）截距。
删剪是否没有信息量？
在生存分析中，一些观测值或个体会被删剪，这意味着我们没有关于他们经历相关事件之前的经过时间的信息（我们只有关于他们被删剪之前的经过时间的信息）。然而，Cox 回归（以及其他形式的生存分析）的一个假设是，被删剪的观测值与个体死亡（经历相关事件）的概率之间没有关系。被删剪的观测值经历相关事件的可能性不应该更大（或更小）。换句话说，这一假设表明--如果被删剪的观测值被实际跟踪，直到他们经历了相关事件--这一生存时间分布将与未被删剪的观测值的生存时间分布相同。
非信息性删剪还意味着观察结果被删剪的原因不应与研究设计有关。考虑一项调查实验药物的临床研究。药物的效果可能非常好，治疗组的个体可能认为自己已经 "痊愈"，不再需要随访（导致这些个体被删剪）。而对照组的人则不会有这种改善，他们将继续参与研究。由于治疗组与对照组的删剪率很高，治疗组的实际生存时间可能无法准确记录，治疗效果也可能无法发现。另外，一种治疗方法也不应该导致患者感觉非常糟糕而选择退出研究（这也不属于非信息性删剪）。
每个观察结果的生存时间是独立的吗？
与许多回归技术一样，一个重要的假设是观察结果是相互独立的。就 Cox 回归而言，每个个体的生存时间必须是独立的。换句话说，个体 1 的存活时间不应依赖于个体 2 的存活时间。
预测（连续）变量相对于对数危险是否是线性的？
Cox 比例风险回归模型的另一个假设是，预测因子变量的影响相对于对数风险是线性的。这句话乍听起来可能令人困惑，但请考虑一下 Cox 回归中使用的危险率方程 (h(t))：
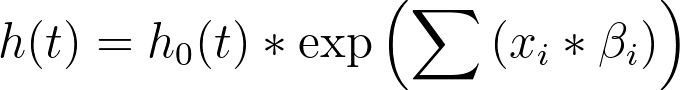
经过重新排列和简化，这个方程可以写成下面的形式：
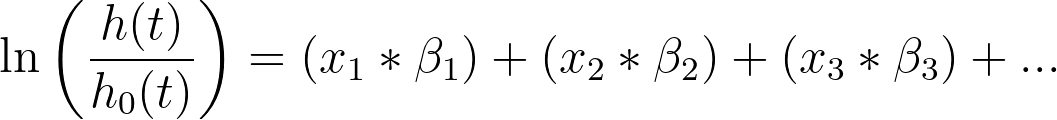
在这种形式下，更容易看出预测因子（x1、x2、x3 等）被假定对对数危险有线性影响。有一些方法可以检查这一假设，比如使用变异性残差图并将其与预测因子变量的值进行对比（此图可使用残差选项卡的选项生成）。使用此图，我们期望看到残差与预测因子变量值的关系没有模式（残差应均匀地以零为中心）。
在预测因子表现出非线性的情况下，有一些方法可以用来修正这种违反线性假设的情况。与其他回归技术一样，一种解决方案是对变量进行变异性转换（例如使用对数或指数转换）。其他可能的方法是在模型中加入变量的多项式项，或将连续变量转换为分类变量。
个体的预测因子变量值是否随时间变化而不变？
Cox 比例风险回归的一个有趣假设是预测变量的值不会随时间发生变化。在使用 Cox 比例风险回归分析的研究中，必然会对个体进行不同时间段的随访（以确定每个个体发生相关事件的时间）。然而，重要的是预测因子变量在这段时间内不会 发生变化。本示例举例说明，如果 "治疗 "是一个预测因子变量，有 "对照组 "和 "治疗组 "之分，那么在研究过程中，个人不得在这两组之间互换（"治疗 "组中的个人应始终在治疗组中），这一点非常重要。在其他类型的多元回归（如多元线性回归）中，数据中没有时间成分，因此不需要这一假设。然而，由于 Cox 回归的数据性质，这一假设的有效性非常重要。
预测变量是否（相互）线性依赖度？
如果模型中的预测因子表现出较高的多重共线性，那么估计的标准误差和 P 值将毫无意义。请阅读有关多重共线性以及 Prism 如何报告模型变量之间这种关系的更多信息。
您是否有足够的数据来相信您的结果？
一般来说，统计建模的数据越多越好。但是，由于各种限制，样本量或人口数量往往有限。表格结果表的 "数据摘要"部分包括输入数据中的一些重要摘要统计。其中，数据中的事件数、指定模型拟合的参数数以及这两个值的比值可用于评估是否有 "足够"的数据来支持所选模型。没有一个特异性的值可以用来明确说明某个模型有 "足够 "的数据，但一般的经验法则是模型拟合的每个参数至少应有 10 个事件。请注意，这不是观测值（删剪和 事件）的比率，而只是每个参数的事件数。还要注意的是，这个比率的分母是模型中参数估计的数量，可能大于变量的数量（由于模型中包含了两个以上水平或交互作用的分类变量）。
是拟合过度还是拟合不足？
与上述观点类似，您指定的模型是否包含了过多（过拟合）或过少（欠拟合）的变量？在对数据进行指定模型拟合后，可能会发现所包含的某些预测变量对风险的变异性没有贡献（换句话说，它们的 β 系数接近或等于零，或者它们的风险比率接近或等于 1）。如果这些变量的值对危险度的变化没有贡献，您是否要将它们纳入模型？在某些情况下，由于这些变量在实验设计中的重要性，或者基于您对实验和相关科学知识的了解，保留这些变量是很重要的。在其他情况下，可能只需将此变量从模型中删除即可，不过这是个有争议的话题，所以在没有经过深思熟虑的情况下不要这样做。
另一方面，模型的拟合优度可能不如人意。这可能是由于你没有测量或选择不在模型中包含一个重要的变异性。在这种情况下，模型被称为 "拟合不足"的数据。如果缺失的变量是你在实验中没有测量到的，那么你能做的就不多了，只能回去收集更多的数据。但是，如果缺失的变量只是在模型中被省略了，你可能需要重新考虑为什么要删除这个变量。此外，您还可以使用参数对话框的 "模型"选项卡，在模型中加入预测因子变量的各种变异性和交互作用。
