Cox 比例风险回归参数对话框的 "残差"选项卡用于生成许多不同的图表,这些图表可以让人深入了解模型拟合的质量,并评估作为分析一部分的某些假设的有效性。
需要注意的是,在 Cox 回归中被称为残差的值并不是传统意义上的残差。在多元线性回归(以及简单线性回归和非线性回归)中,残差被定义为同一观察值的结果变量观察值与结果变量预测值之间的差值。例如,如果利用个人的年龄、性别和体重变量生成了一个多元线性回归模型来估算个人的身高,那么您可以比较用于构建模型的每个测量身高,以及该模型利用相同的年龄、性别和体重输入值预测的相应身高。这两个值(观察值和预测值)之间的差值就是残差。
遗憾的是,这种 "实际值减去观察值 "的概念并不能直接用于 [Cox 比例风险回归]。相反,人们提出了一些不同的值,试图在 Cox 比例风险回归中回答与标准残差对其他类型回归(如多元线性回归)所回答的相同问题。
比例风险假设是否有效?
其中第一个问题是问比例风险假设是否有效。这一假设本质上是指,所研究人群中任意两个个体的风险比将随着时间的推移而保持恒定(参见指南本节中的风险示例)。为了检查该假设的有效性,Prism 提供了两种图表:缩放舍恩菲尔德残差与时间或行序的关系图,以及对数减对数生存图。
•缩放舍恩菲尔德残差与时间/行序的关系 - 如果比例风险假设成立,这些残差应随机分布在以零为中心的水平线上。如果这些残差有明显的趋势,则很可能违反了比例风险假设。请注意,删剪观测值不存在缩放的舍恩费尔德残差。
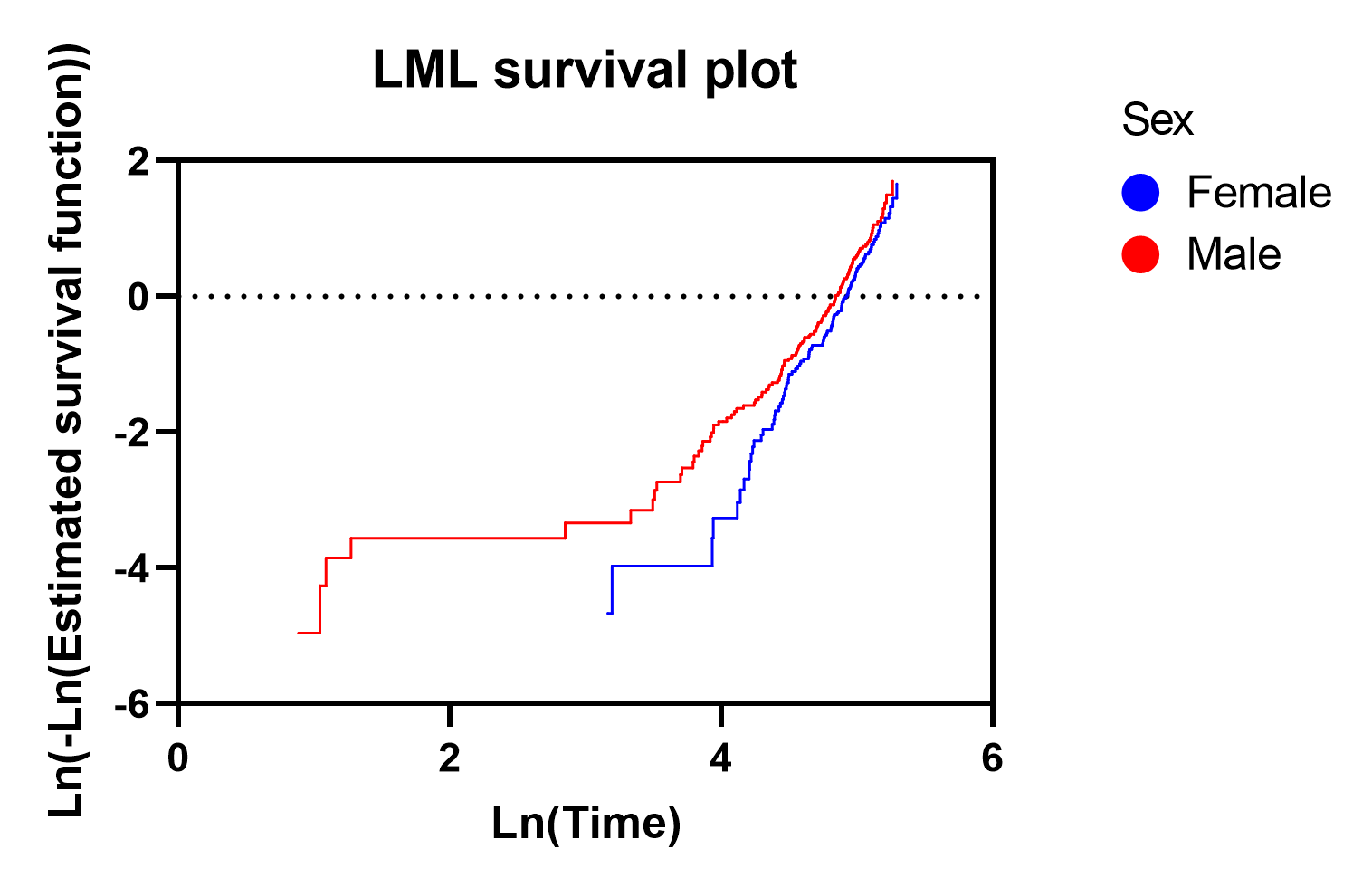
•对数减对数(LML)生存图--如果指定模型包含分类变量,则可通过此图的选项选择这些分类变量来绘制 LML 图。该图包含所选分类变量中每个组(水平)的一条曲线。在绘制这些曲线时,会使用 Nelson-Aalen 危险估计来计算每个组的累积危险。回顾累积危害 H(t) = -Ln(S(t))。对每个组的 Nelson-Aalen 累计危险估计值取自然对数,就得到 Ln(H(t)) 或 Ln(-Ln(S(t)))。这就是图名所指的 "对数减对数 "值,它被绘制在 Y 轴上,Ln(时间)被绘制在 X 轴上。如果比例风险假设成立,单一分类预测因子变量的各组(水平)曲线将大致平行。下图是 LML 图,比较了 "女性 "和 "男性 "的曲线。虽然该图中的两条线并不完全平行,但它们表明本分析并没有严重违反比例风险假设。如果单一分类预测变量的各组(水平)曲线相互交叉,很可能已经违反了分析的比例风险假设。
注意,在创建 LML 图时,Prism 还会包含未经转换的 "时间 "和 "预测生存函数 "值,这些值可以绘制在图的 X 轴和 Y 轴上。对于指定的分组变量,结果是每个选定组/级别的标准非参数生存曲线。
观测值中是否存在异常值?
为了检测分析输入数据中潜在的异常值,人们提出了许多不同的 Cox 比例风险残差图。
•离差残差与线性预测因子/HR - 此图上的点应大致以零为中心,而残差绝对值较大的点可能代表异常值。请注意,在这些图表中观察到的趋势可能是由于样本量不足或观察结果的删剪方式模式造成的。
•马丁格尔残差与线性预测因子/HR - 与偏差残差一样,这些残差可用于查找数据中的潜在异常值。不过,这些残差是偏斜度的(不以零为中心),事件观测值的残差范围为(-inf,1],而删剪观测值的残差范围为(-inf,0]。这些残差通常比偏差残差更难解读。请注意,在这些图表中观察到的趋势可能是由于样本量不足或观测值删剪方式的模式造成的。
•Schoenfeld 残差与时间或行序的关系 - 与偏差和 Martingale 残差不同,这些残差用于确定观测值对每个回归系数的影响。选择该残差时,将生成一个图形,让您检查每个变异性变量系数的 Schoenfeld 残差。该图还可用于检验比例风险假设(如果这些图显示出非零斜率,则可能违反了比例风险假设)
预测因子是线性的吗?
Prism 提供了两种图表,可用于评估预测因子变量对模型影响的线性程度。与调查异常值可能存在的图表一样,可以使用偏差残差或马丁格尔残差。
•偏差残差与共变量对比图--这将生成偏差残差与模型中每个连续预测变量的对比图。与之前一样,离差残差预计会随机地以零为中心。这些残差的趋势可能表明所选预测因子变量偏离了线性。
•马丁格尔残差与协变量--这些残差是偏斜的,落在 (-inf, 1] 的范围内,但平均值仍应为零。这些残差的明显趋势可能表明所选预测因子变量偏离了线性。这些残差通常比偏差残差更难解读
拟合优度如何?
提供这些残差图只是为了将 Prism 生成的结果与其他统计软件包生成的结果或以前发表在文献中的结果进行比较。Cox-Snell 残差是最早为 Cox 比例风险回归开发的残差之一,目前已基本被本页列出的其他残差所取代。
•累积危险率的 Cox-Snell 与Nelson-Aalen 估计值对比图--该图最初建议用于评估模型的整体拟合度。拟合良好的回归结果会在此图上产生一条近乎直线的点,这条直线穿过原点,斜率为 1。然而,此图的问题在于,如果模型的拟合度特别差,生成的可视化效果就不会是这个样子,而且也无法深入了解拟合度差的原因(违反比例风险假设、异常值、因变异性变量等)。