首先，让我们来定义一下危险率，它是指在相关事件尚未发生的情况下，在单位时间内发生的频率。危害率越高，表示在一定时间内发生的事件越多，而危害率越低，表示在一定时间内发生的事件越少。重要的是，危害率会随着时间的推移而变化。以下面的示例图表为例：

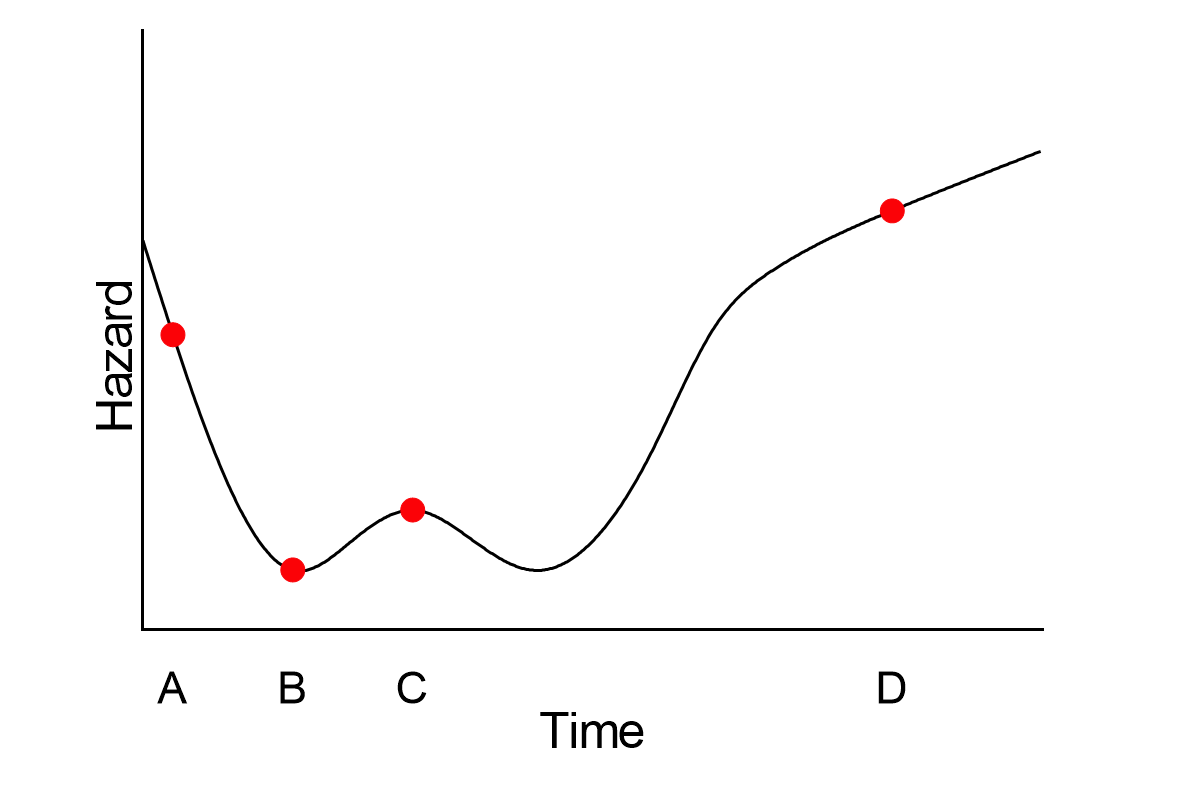
在这幅图中，危险开始时有点高，然后在最初的一段时间内有所下降。然后上升到一个小高峰，再次下降，最后在观察期结束时以不同的速度上升。对这张图的解读是，在时间点 A 处发生事件的风险高于 B 处；在时间点 C 处发生事件的风险低于 A 处，但高于 B 处；在 D 处的风险高于 A、B 或 C 处。

虽然这张图是理论上的，但它确实与人类预期寿命中的实际危险率有一些相似之处。出生时的死亡危险率实际上比出生后不久的死亡危险率要高得多。这种危险率在十几岁到二十几岁时迅速上升（男女略有不同），然后随着时间的推移继续上升。

需要注意的是危害和事件发生时间信息之间的关系。如果将观察到的事件发生时间数据视为离散数据（即事件只能发生在确定的时间点上），那么危害的定义就相对简单。由 h(t) 得出的危害定义如下

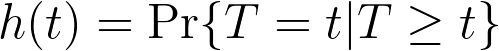
其中，"T"是一个变量，表示事件可能发生的经过时间，"t"表示感兴趣的特异性时间。垂直线"|"是概率符号，意思是 "鉴于"。因此，换句话说，危险率就是事件 "T"在时间 "t"发生的概率，"给定 "它在时间 "t "之前没有发生。然而，当时间被视为连续时（生存分析中几乎总是如此），情况就会变得复杂一些。由于时间是连续的，事件可能发生在任何给定的瞬间。在任何确定的时间窗口中，都有无数个可能的 "瞬间"。由于微积分的性质，这意味着事件发生在任何一个特异性瞬间（T=t）的概率实际上为零。如果不能马上理解，也不用太担心，只需知道当时间被视为连续变量时（如在 Cox 比例风险回归中），计算风险所需的数学就会复杂一些。

在后面的章节中，我们将通过大量的数学计算来说明危害函数和生存函数是直接相关的。不过，在不涉及细节的情况下，我们需要知道的重要一点是，建立危险函数模型比直接尝试建立生存函数模型更简单、更方便。因此，Cox 比例风险回归的对象就是估计危险函数。根据这个危险函数，就可以生成生存函数（以及生存率的估计/预测）。