Cox 比例风险回归的目的是利用观察到的时间到事件数据，在预测因子变量值与风险率（风险函数）之间建立数学关系。根据这些信息，可以确定存活率函数，从而估算出每个人随时间变化的存活率。不过，为了数学上的简便，实际建模的是危险率。下面是 柬埔寨比例风险回归所要定义的一般模型：

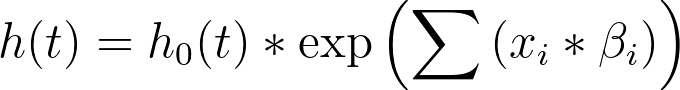
其中

•h(t) 是危险率（作为时间的函数）

•h0(t) 是基线危险率（定义如下）

•xi是每个预测变量 i 的值 - 请注意，在 Cox 回归中，每个观察值到相关事件的经过时间不被视为预测因子变量。相反，预测变量代表可能对该经过（生存）时间有影响的任何其他测量变量

•βi是每个预测变量 i 的系数。

Cox 比例风险回归最重要的一点是基线风险假设，即上式中的h0(t)。它本身是一个时间函数，代表了相关事件发生频率与时间之间的关系曲线（如上一节所示）。重要的是，基线危险的特异性形状并不重要（它可能一开始很高，然后随着时间的推移而降低；也可能一开始很低，然后随着时间的推移而升高；或者它可能自始至终包含许多波峰和波谷）。事实上，进行 Cox 比例风险计算根本不需要了解基线风险率的形状或属性。基线风险可以采用任意分布的这一假设使 Cox 比例风险成为一种半参数分析。

要了解基线危险度的关键点在于，它代表了所有预测因子变量的值都设为零时的危险度（或分类变量的参考水平）。这可以用上面的公式表示，将xi设为零：

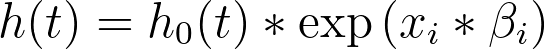
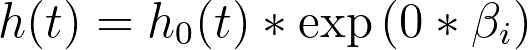
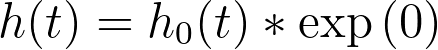
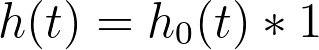
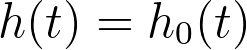
因此，基线危险度就是所有预测因子变量值设为零时的危险度函数！将基线危害值乘以由预测变量特异性值决定的某个量（即上文危害率等式中的 "exp(Σ(xi*βi)) "部分），就可以得出人群中任何个体的危害值。另一种说法是，任何个体的风险率都与共同的基线风险率成比例。

基线危险函数这一假设的另一个非常有趣的结果是，当我们考虑两个具有不同预测因子变量值的个体的危险时会发生什么。为了简单起见，让我们考虑一个具有单一预测因子变量（xi）的模型，其中一个人的该变量值为 "a"，而第二个人的该变量值为 "b"。这两个人的危险函数为

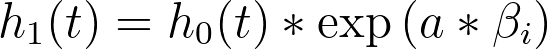
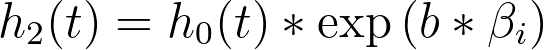
这两个人的风险函数比为

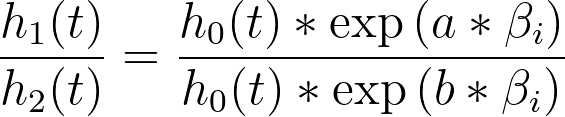
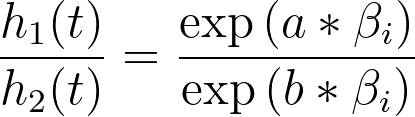
分子和分母中的基线危险相抵消，剩下一个与时间相关的恒定分数（我们假设预测变量的值不会随时间变化）。换句话说，人群中任何两个个体的风险比在任何时候都是恒定的。还有一种说法是，人群中两个个体的风险总是成比例的。这种比例的概念就是这种分析法的名称：Cox 比例风险回归。下图给出了这些比例关系的示例图表：黑色曲线是理论上的基线风险率，而蓝色和红色曲线则代表与单一预测因子变量的两个不同值（蓝色曲线为某个任意值 "α"，红色曲线为该值的两倍 "2α"）相对应的风险率：

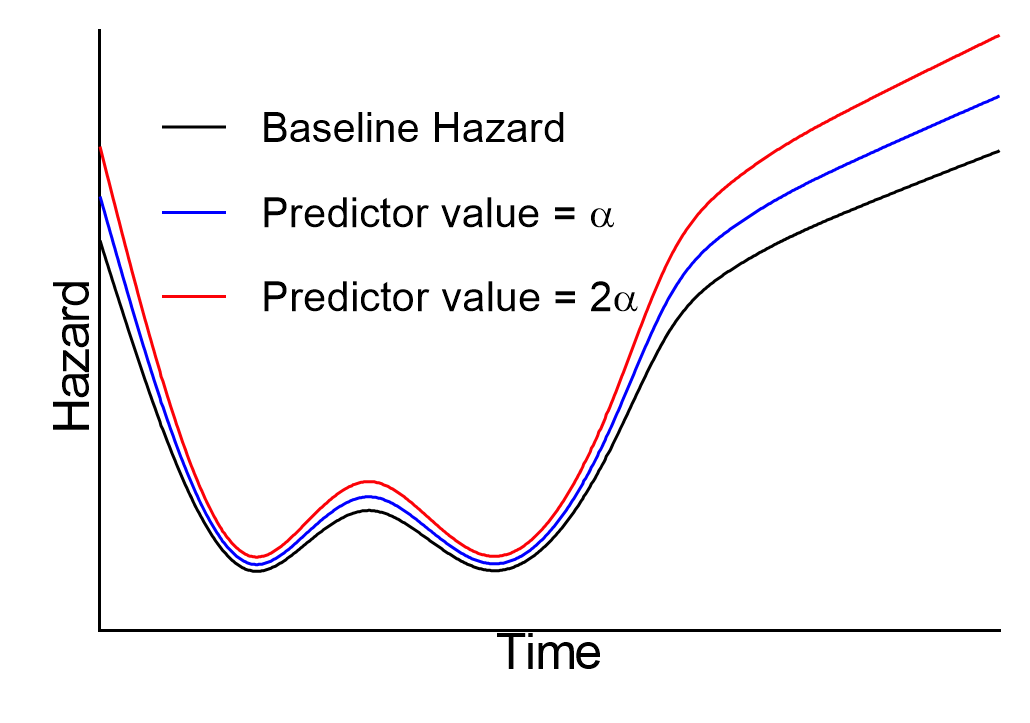
可以看出，在所有时间点上，每条曲线之间的垂直距离并不是恒定的，而是在任何时间点上任意两条曲线的风险比都将保持不变。因此，随着基线危险值的增加，曲线之间的距离也会增加，而每条曲线都保持相似的形状，重要的是，这些曲线永远不会交叉。

在后面的章节中，我们将深入探讨这些危险率与存活率函数之间的数学关系，在给定模型中一组预测因子值的情况下，存活率函数可用于绘制人群中任何个体在整个研究期间所有时间的估计存活率。