生存分析是研究特异性事件发生前的时间量的过程。在许多实验（尤其是生物科学实验）中，受试者（小鼠、细胞等）的死亡往往是感兴趣的事件。这些实验的反应变异性是受试者存活的时间（这也是该分析的名称由来）。然而，生存分析同样适用于其他类型的实验，如测量机械零件从使用到损坏或失效所需的时间，或测量学生获得学位所需的时间。在这些情况下，分析可能有不同的名称（在经济学中，这些分析可能被称为 "持续时间分析"或 "持续时间建模"；在社会学中，这些研究可能被称为 "事件历史分析"）。然而，所有这些分析在本质上是相同的。

生存分析的主要成果之一是了解生存概率是如何随时间变化的。这种关系可以用生存曲线的形式用图表表示出来。这些曲线是针对特定人群生成的，在 X 轴上绘制经过的时间，在 Y 轴上绘制生存概率（分数或百分比）。因此，曲线的位置被定义为相关人群中的个体在不发生相关事件的情况下 "生存"一定时间的概率。请看下图所示的生存曲线本示例：

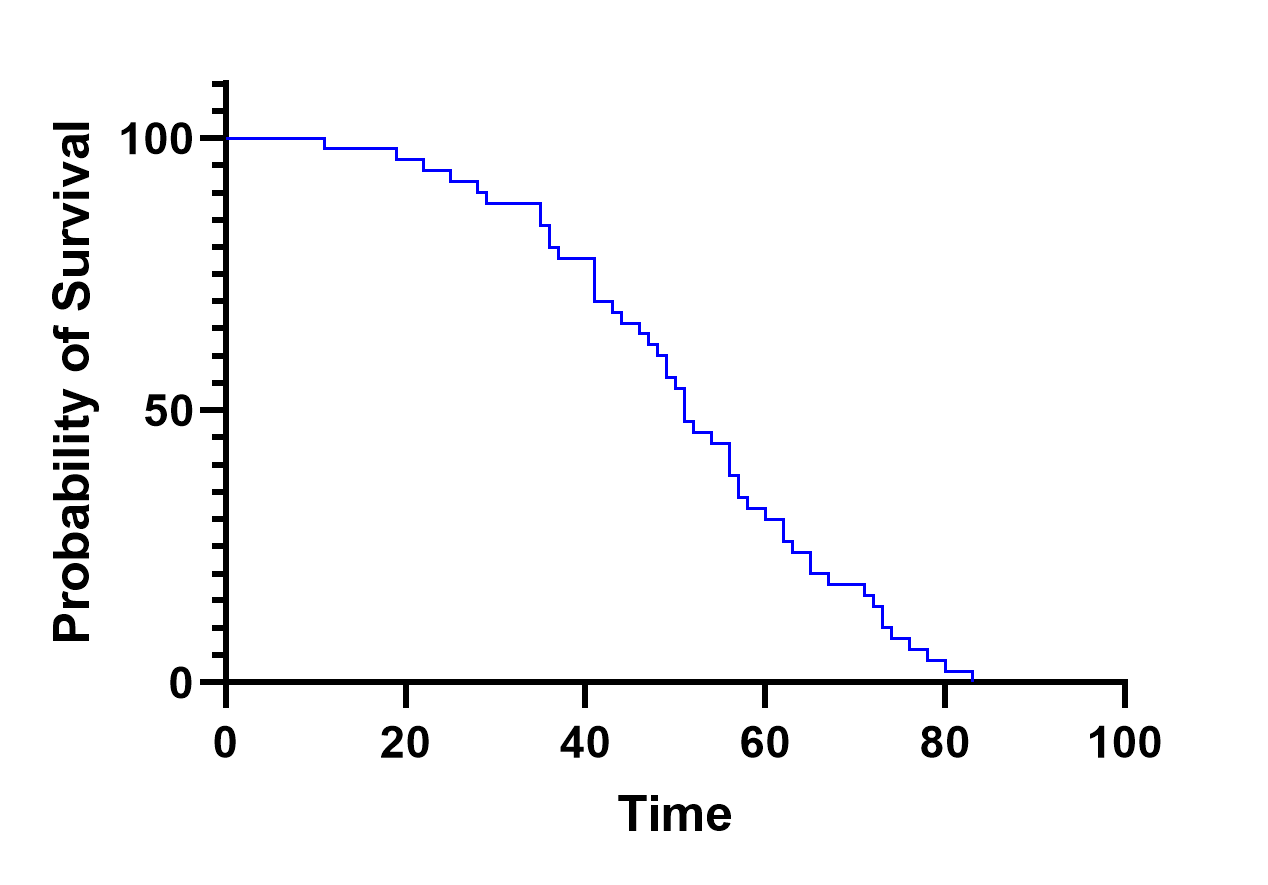
在这张图中，我们可以看到典型的 "阶梯式"生存曲线斜率。在该图中，存活概率以百分比表示，从零时的 100%开始，到 83 天左右的 0%结束。这种 "阶梯"形状是生存概率计算方式的结果：生存概率只有在人群中有人经历相关事件（当相关事件是死亡时，这些时间点就是个人死亡的时间点）时才会发生变化，因此这些垂直下降的每一个点都代表了研究人群中的一个事件。这些图表可以用来确定单一人群的重要信息，如中位生存时间，也可以用来统计比较多个人群，每个人群都有自己相应的生存曲线。

上面的曲线是使用Kaplan-Meier 方法绘制的，本指南的这一部分将介绍如何在 Prism 中执行 Kaplan-Meier 生存分析。

另一种生存分析技术--Cox 比例风险回归--也可在 Prism 中使用，本指南的这一部分将解释如何执行该技术。