在生存分析中，响应变量是指从某个定义的 "起始时间"到另一个定义的 "终点"之间所经过的时间。由于这类研究中常见的 "终点"是受试者死亡，因此这一经过的时间通常被称为生存时间。几乎所有类型的生存分析，其主要对象都是估计或了解该响应变量与一个或多个预测因子变量之间的关系。这些预测因子变量可能是实验条件规定的变量（如接受一种治疗与接受另一种治疗或对照），也可能是观察变量（如研究对象的性别）。

本示例中，生存分析可用于研究癌症新疗法的效果，方法是测量接受新疗法的个体与接受标准疗法的对照组个体的生存时间。通过比较每组患者的存活时间，可以获得有关新疗法疗效的信息。

再举一个生存分析的本示例，假设你在一家公司工作，该公司生产一种用于全国不同实验室的实验设备。你的任务是研究设备中一个特异性部件的故障。除了测量每个设备在组件失效前的使用时间外，您可能还会记录每个实验室内的环境温度和相对湿度（假设这些参数不会随时间发生变化）。在本示例中，生存分析可以让您研究温度（或湿度）与设备内元件失效时间之间的潜在关系。

一旦确定了预测变量和存活时间之间的关系，这些信息也可以用来估算其他受试者或个体随着时间推移的存活概率（假设这些个体的预测变量值是已知的）。

 

这听起来很像多元线性回归

如果您熟悉多元线性回归模型，那么生存分析似乎也在试图实现同样的目标（即揭示某些测量响应变量与一组预测因子变量之间的关系）。而且，正如本指南稍后将说明的那样，多元线性回归与某些生存分析技术（参见：Cox 比例风险回归）之间存在一些相似之处。然而，生存数据有一些重要特征，导致典型的多元线性回归方法不适合分析这类数据。

生存数据通常具有高度偏斜度

如前所述，生存分析的响应变量是每个观察对象（受试者、个体等）在达到某个定义终点之前所经历的时间。这对响应变量值的分布有一些重要影响。首先，由于我们测量的是经过时间，所以所有的值都是正值（生存分析中不存在 "负时间"）。其次，在观察或采样生存时间时，所得到的值一般会高度偏斜。下面的直方图显示了一组 5000 个观测值的存活时间

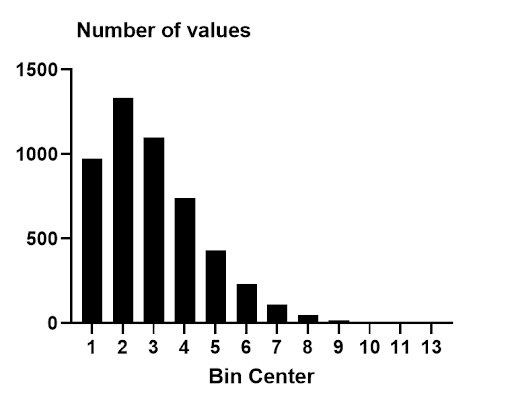
大部分存活时间位于时间 1 和 3 之间（近 70% 的观察存活时间位于此范围内）。不过，也有多个观测值远至时间 13。据说，直方图右侧的这些数值使分布具有 "较大的右尾部"，或者说分布是 "右偏斜度"的。这些数据是模拟数据，但却显示了真实生存数据中经常观察到的右偏斜度分布的特征。由于这种偏斜度，许多依赖于正态（高斯）分布的假设和技术都无法使用。

删剪数据

生存分析与标准线性回归技术的另一个主要区别是删剪数据的普遍存在。这是生存分析中一个非常重要的话题，因此在指南中也有自己的一页。