在进行回归时，强相关的预测因子变量（或更普遍的线性依赖度预测因子变量）会导致估算的不稳定性。这通常意味着无法准确解读回归产生的估计值。其原因在于--当两个预测变量为线性依赖度时--一个变量可以用来预测另一个变量的值。另一种说法是，一个变量可以写成另一个变量的线性函数。例如，如果公式 X2 = 3*X1 + 6 为真，预测因子 X1 和 X2 将是线性依赖度变量。对于任何给定的 X1 值，X2 的值都是已知的（因此无需估算）。如果是这样的话，加入 X2 就不会给模型增加任何无法用 X1 描述的新信息。

在多重回归分析中，这个问题被称为多重共线性。在极端情况下，当一个预测变量与另一个预测变量完全线性依赖度时，完成分析所需的优化算法无法确定任一列的系数估计值。这是因为这些参数估计有无数个可能的解。为了使这一概念更加清晰，可以举一个本示例：在一个数据集中，两个变异性变量都包含体重值，一个以磅为单位记录，一个以公斤为单位记录。由于这两个值完全线性相关（磅 = 2.205* 千克），因此同时包含这两个值的模型将无法确定其中任何一个的参数估计值。

考虑一下下面的 Cox 比例风险回归案例。假设只有一个预测因子变量（x1），这个预测因子变量的拟合优度参数估计为 2。Cox 回归模型为

 

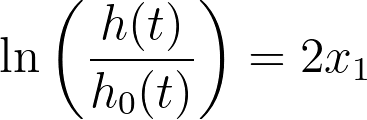
现在，假设我们增加了一个新变量（x2），它是第一个预测因子变量的拷贝。由于x1=x2，可以看出下面所有的方程都等价于第一个方程：

 

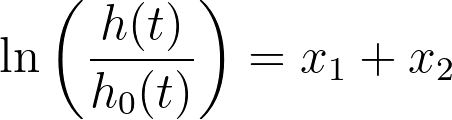
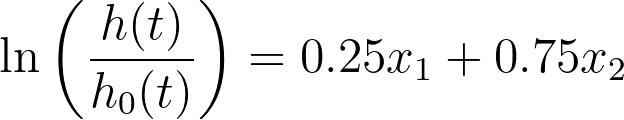
事实上，有无数种方法可以用不同的系数重写这个等式，但结果都是相同的。在统计学中，这种模型被称为不可识别模型。在这种极端情况下，根本无法计算标准误差、置信区间和 P 值。

不过，在实践中更常见的情况是，预测因子之间并非完全线性依赖度，而只是强相关。虽然 Prism 能够在这些情况下生成参数估计，但问题仍然存在，即多重共线性增加了参数估计的不确定性。这可以从更宽的置信区间和更大的 P 值中看出。

如果您唯一关心的是使用模型来预测一组确定的预测因子变量值的未来结果，那么大的标准误差和较宽的置信区间可能不是主要问题。但是，如果您对参数估计值大小的解读感兴趣，那么多重共线性就是一个问题。

在 Prism 中，多重共线性使用方差膨胀因子（VIF）进行评估。一般来说，VIF 超过 10 表示多重共线性很强，很可能不利于模型拟合。在 VIF 值达到这种程度的情况下，您可能需要移除其中一个 VIF 值较高的预测因子变量，然后重新构建模型。必要时可以重复上述操作。本页提供有关 VIF 的更多详细信息。