在进行任何类型的回归时,通常都需要研究与其他可能的拟合模型相比,模型对数据的描述程度如何。Prism 提供了多种方法,可用于提供有关模型与所提供数据拟合程度的信息。具体来说,对于 Cox 比例风险回归,Prism 会报告 Akaike 信息准则 (AIC)、部分对数似然 (LL)、部分对数似然的变换 (-2*LL) 和伪 R 平方的值。
阿凯克信息准则(AIC)
该值由信息论方法得出,试图确定数据与模型的拟合值。所报告的值既依赖于部分对数似然(如下所述),也依赖于模型中参数的数量。请注意,由于在存在删剪的情况下很难指定观测值的数量,Prism 和其他应用程序一样,只报告 AIC,而不报告校正 AIC (AICc)。计算 AIC 所需的公式如下:
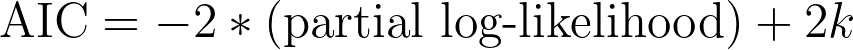
其中 k 是模型中的参数数(由 Prism 在结果的数据摘要部分报告)。
解读 AIC
AIC 的解读在很大程度上依赖于模型拟合的似然(更特异性的是对数似然,或者在 Cox 回归中是部分对数似然)概念。在此不对似然背后的数学知识做过多解释,一般的想法是,一个模型的似然可以告诉您数据与该模型的拟合程度(另一种想法是,如果假设所选模型是"真正的"模型,那么这些数据产生的"可能性"有多大)。有鉴于此,"好"模型的可能性值越高,而"差"模型的可能性值越低就越合理。
在上面的等式中,我们可以看到 AIC 依赖于两方面:
1.模型的偏对数似然值
2.模型中参数的数量 (k)
Cox 回归模型的部分对数似然就是部分似然的对数。如上所述,数据拟合度较高的模型比数据拟合度较低的模型的似然值要高。因此,数据拟合度较高的模型的部分对数似然值也会大于数据拟合度较低的模型的部分对数似然值。通过将该值乘以负值,我们可以看出,数据拟合较好的模型的"-2*(部分对数似然)"值将小于数据拟合较差的模型的"-2*(部分对数似然)"值。因此,我们可以看到,较大的似然最终会导致较小的 AIC(忽略即将讨论的 2k 项)。因此,较小的 AIC 代表"较好的"模型拟合度是有道理的。
AIC 等式的第二部分是一个"惩罚"项,用于防止过度拟合(在模型中使用过多参数)。对于任何模型,添加额外的参数(不改变任何其他参数)通常总是会增加模型拟合结果的可能性。只要有足够多的参数,就能完美预测输入数据集中的数据(但这个模型几乎肯定无法预测输入数据之外的未来观察值)。这就是过度拟合的问题:模型与输入数据拟合得太好 。AIC 公式增加了一个值,等于模型中参数数量的两倍(2k),因此参数越多的模型,其 AIC 值增加的"惩罚"也就越多。
利用所有这些信息,我们可以开始进一步理解 AIC:
•在相同数据上,AIC 值小的模型比 AIC值大的模型拟合值更好
•参数越多的模型似然值越大,但其 AIC 值的"惩罚"也越大
关于 AIC 值,最后一个需要注意的非常 重要的概念是,AIC 值只能在拟合相同数据的模型之间进行比较!AIC 值是根据似然率计算出来的,而似然率是针对所分析数据集的特异性。因此,尝试比较拟合不同数据集的模型的 AIC 值没有任何意义。还要注意的是,我们用来评估一个拟合模型比另一个"更好"或更差的是 AIC 的差异,而不是 AIC 值的比率。这个比值不能直接解读,所以不做报告。
因此,解读 Prism 中报告的 Cox 回归 AIC 的最佳方法是将指定模型提供的 AIC 值与拟合相同数据的空模型或另一个(竞争)指定模型的 AIC 值进行比较。在与空模型比较时,所选模型的 AIC 值越小,说明所选参数改善了模型的拟合效果。当比较两个相互竞争的模型时,在考虑每个模型所含参数数量的情况下,具有 AIC 的模型被认为整体拟合效果更好。
关于 AIC 的高级信息
在比较模型时(例如,比较同一数据的两个竞争模型或比较指定模型与空模型),可以使用每个模型的相应 AIC 值来计算每个模型正确的"概率"(假设这些是唯一 可能的模型,因此其中一个模型一定是正确的)。为此,我们可以使用两个 AIC 值之间的差值。首先,我们为每个模型定义一个新值:
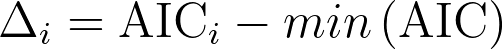
其中AICi是单个模型的 AIC,min(AIC) 是所比较模型的所有可能 AIC 值中的最小值。请注意,对于 AIC 值最小的模型,AICi将与 min(AIC)相同,因此该模型的Δi将为零。一旦我们得到了每个模型的 Δ 值,就可以用下面的公式计算出每个模型正确的"概率":
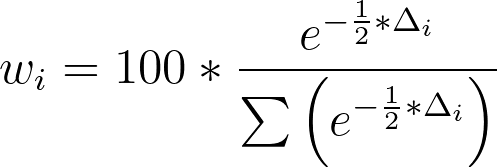
本示例中,考虑比较具有以下 AIC 值的两个模型:
•模型 1 AIC:283
•模型 2 AIC:285
因此,这些模型的 Δ 值为
•模型 1 Δ:0
•模型 2 Δ: 2
每个模型正确的概率计算如下
•模型 1 w: 73.11
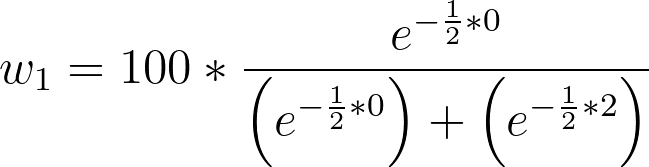
•模型 2 w: 26.89
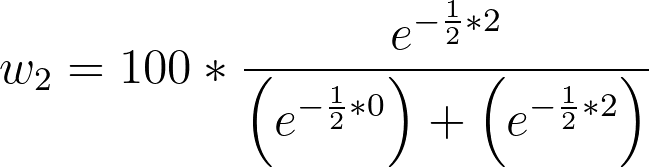
这种方法可以扩展到对任意数量的模型进行比较,但请记住,这种方法的假设是,被比较的模型之一是"真正的"模型(尽管这种假设在实践中可能并不完全正确)。
部分对数似然法 (LL)
似然的概念在数学上相当复杂,在估计拟合优度参数值的过程中使用,是 Cox 比例风险回归分析的一部分。然而,偏对数似然用于评估模型拟合度的方法(幸运的是)非常简单。一般来说,在比较拟合到相同数据的两个模型时,对数似然值较大的模型被认为"拟合"得更好。请注意,这些对数似然值通常为负值!在这种情况下,较大的值与较小的负值相同。因此,负值较小的模型被认为是"拟合"较好的模型。
选择该选项后,结果中将给出无协变量模型(空模型)和指定模型的部分对数似然值。如果所选模型的部分对数似然值小于空模型的负对数似然值,则意味着输入数据由指定模型生成的可能性大于空模型。不过,一般是用每个模型的 AIC 值来确定哪个"更好"(AIC 值越小代表模型拟合值越"好")。
负 2 倍偏对数概率 (-2*LL)
与 Prism 在本节结果中报告的其他值一样,该值与偏对数似然相关,可用于评估模型与给定数据的拟合值。如前所述,在计算 AIC 时会直接使用"-2*(部分对数似然)"这个值。幸运的是,一旦获得了部分对数似然(由 Prism 报告),计算这个值就像乘以 -2 一样简单!其他程序和书籍有时会以其他等效方式报告该公式:
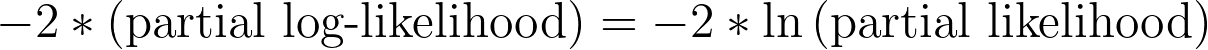
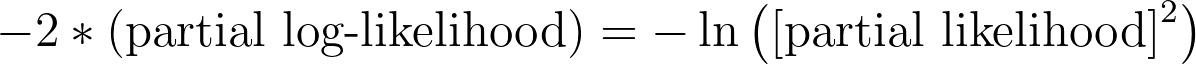
伪R2
在考虑回归分析的"拟合优度"时,通常会提到 R 平方的概念。该指标提供了模型解释方差的估计值,在进行多元线性回归时非常有用,但对于 Cox 比例风险回归,没有办法计算相同的指标。因此,人们提出了其他一些"伪 R 平方"类似值。请注意,这些值的数学解读与 R 平方并不相同。伪 R 平方值并不代表指定模型所解释的方差比例。相反,这些伪 R 平方值通常用于比较同一数据上多个模型的拟合优度。
如果在"Cox 比例风险回归"的参数对话框中进行选择,Prism 将报告 Cox-Snell 的 R 平方(有时称为"广义"R 平方)。该值是使用指定模型和空模型(无协变量模型)的似然值按以下公式计算得出的:
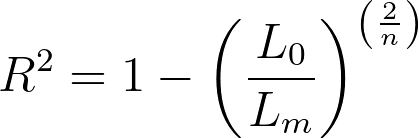
其中,Lm是指定模型的部分似然值(注意,不是对数似然值),L0是无协变量模型(空模型)的部分似然值,n 是模型中使用的观测值的数量(包括删剪观测值)。
从这个伪 R2 的等式中我们可以看出,当一个模型与数据拟合值较好(Lm 的部分似然值较高)时,分数会变小,R2值也会变大。当给定模型的部分似然值较小时,分数会变大,相应的R2值也会变小。与正常(最小二乘)回归中的R2值一样,该公式的最小值为 0(如果指定模型的部分似然与空模型相同,则R2等于零)。然而,与标准R2 不同的是,这个伪R2 的上限不是 1!相反,如果模型完全拟合数据,并且模型的似然值为 1,那么得到的等式就是:
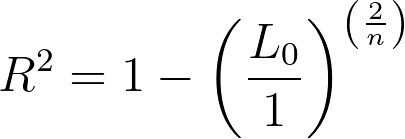
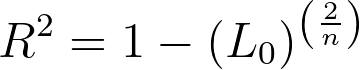
无效模型的部分似然一般极小,但不为零。因此,Cox-SnellR2的最大值依赖于无效模型的似然度,可能非常接近 1(有时接近到计算机无法计算其差值),但不一定等于 1。
总而言之:
•该伪R2的最小值为 0.0
•该伪R2的最大值小于 1.0,但在很多情况下非常非常接近 1.0