这是一个重要的选项卡,有三个大的选择:如何报告参数的置信区间,是绘制曲线的置信带还是预测带,以及当数据没有提供足够的信息来拟合所有参数时该怎么办。
参数置信区间
如果您想运行非线性回归的原因是为了插入未知值,那么您不会真正关心参数的值,因此也不会关心参数的置信区间。但如果您确实关心参数值,我们建议您始终要求 Prism 报告置信区间,因为检查拟合优度参数的置信区间是评估任何非线性拟合的重要部分。
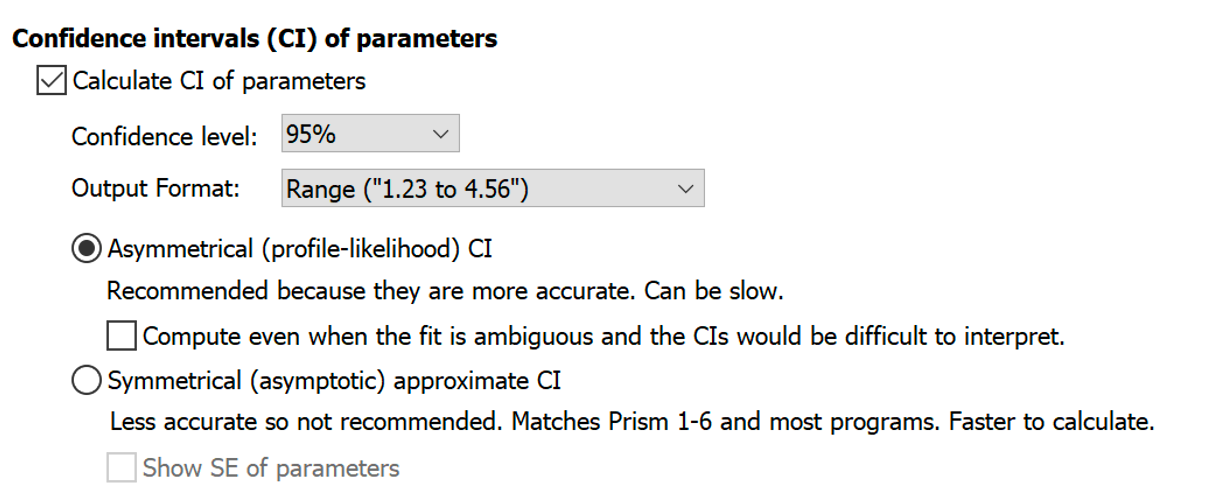
置信水平和输出格式
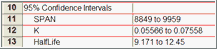
置信区间传统上通常按 95% 置信度计算,但您也可以选择其他置信水平。
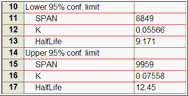
Prism 可以以两种方式报告置信区间:作为一个范围或作为置信下限和置信上限的单独块(如果要将结果粘贴到其他程序中,则非常有用)。前者更容易阅读。如果要在其他地方将结果制成表格,后者可能更好。
|
|
如何计算区间
Prism 提供了两种计算置信区间的方法。不要将这里的两种选择与报告参数变换 CI 的两种选择混淆。
•不对称 剖面似然置信区间(因此更准确) 。我们推荐这一选择,因为它能更好地量化您对参数值的精确了解程度。不确定性往往是不对称的,因此最好使用能报告不对称区间的方法。唯一的缺点是计算比较复杂,因此在使用庞大的数据集时(尤其是用户自定义方程时)明显较慢。
•渐近近似对称置信区间。这些也称为 Wald 置信区间。这些是 Prism 6 及更早版本和大多数程序所报告的唯一置信区间。但由于参数值的真实不确定性往往是不对称的,因此这些对称区间并不总是准确的。我们建议,只有当您需要将 Prism 的结果与其他程序进行比较时,当您需要与早期工作保持一致时,或者当您的数据量太大,剖面似然法的速度太慢时,才选择它们。
如果选择渐近对称置信区间,还可以要求 Prism 报告参数的标准误差。标准误差是用于计算对称置信区间的中间值,但本身意义不大。您可能希望在结果中包含标准误差,以便将 Prism 的结果与另一个不报告置信区间的程序的结果进行比较,或者与不了解置信区间的同事进行合作。但我们建议按惯例关闭标准误差的报告,因为标准误差不能很好地表达拟合优度参数值的精度。从 8.2 版开始,只有当您选择报告对称置信区间时,Prism 才会提供报告标准误差值的选择。
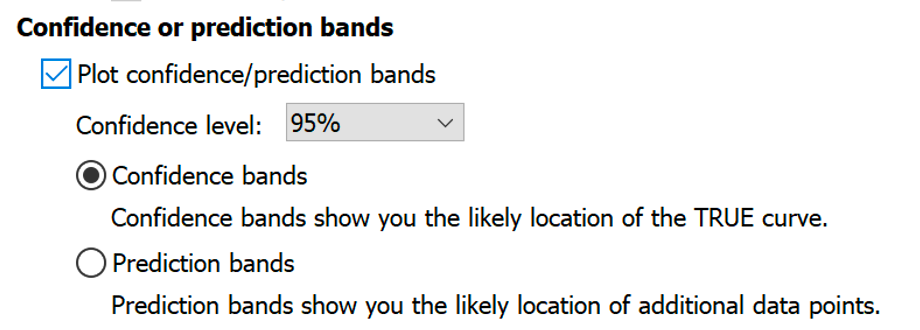
置信带和预测带
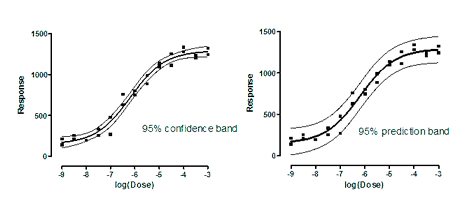
95%置信带包围了您可以确定 95% 包含真实曲线的区域。它可以让您直观地了解您的数据在多大程度上定义了拟合优度曲线。
95%预测带包含了您期望包含 95% 未来数据点的区域。这既包括曲线真实位置的不确定性(由置信带包围),也考虑了曲线周围数据的分散性。因此,预测带总是比置信带宽。当数据点较多时,差异就会很大。
不稳定的参数和模糊拟合

有时,您的数据根本无法很好地定义模型。Prism 提供三种方法来处理这种情况。
•识别不稳定参数。从 Prism 9.0 开始,这是默认选项。另一种方法(识别 "模糊"拟合,见下文)使用依赖度大于 0.9999 的标准。在极少数情况下,依赖度可能>0.9999,但仍有可能获得有用的参数拟合优度值和有用的置信区间。我们基于依赖度的 "模糊"方法并没有报告这些参数的任何结果。我们的新方法工作方式完全不同,可以为数据集找到 "模糊拟合"方法无法找到的最佳拟合值或置信区间。适用时,Prism 将显示 "不稳定"字样,以代替该参数的最佳拟合值和置信区间。
•识别 "模糊"拟合。这是 Prism 7.0 至 8.1 一直使用的方法。如果希望结果与旧版本保持一致,这种方法非常有用。如果任何参数的依赖度大于 0.9999,Prism 就会将拟合标记为 "模糊",在拟合优度值前加上斜杠 (~) 以示不可信,并且不显示其置信区间。进一步了解 Prism 如何计算依赖度。
•两者都不无论如何,只要报告拟合优度值即可。大多数其他程序都是这么做的。