什么是依赖度？

当模型有两个或更多参数时（几乎总是这种情况），这些参数就会相互交织在一起。

参数相互交织意味着什么？拟合模型后，改变一个参数的值，但不改变其他参数。曲线会远离点。现在，尝试通过改变其他参数，使曲线回到接近点的位置。如果能使曲线更靠近点，说明参数是相互交织的。如果能使曲线回到原来的位置，那么参数就是多余的。

Prism 可以通过报告相关矩阵或报告依赖度来量化参数之间的关系。

解读依赖度

您可以在不太了解计算方法的情况下解读依赖度。如果您有兴趣了解该值的计算方法，请继续阅读。

依赖度计算本示例

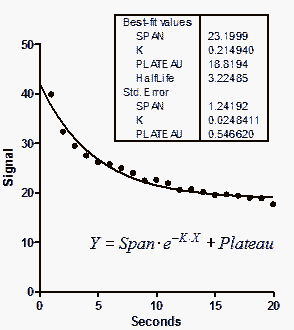
本示例为指数衰减（摘自《MLAB 应用手册》第 128-130 页，www.civilized.com。

 

拟合优度值为 0.2149 秒-1，对应于 3.225 秒的半衰期。其 SE 为 0.0248 秒-1，对应的 95% 置信区间为 0.1625 至 0.2674 秒-1。

很明显，这三个参数并不完全独立。如果强行将K设为更高值（衰减更快），曲线将离点更远。但是可以通过让曲线以一个较高的值开始，以一个较低的值结束（增加跨度，减少高原）来进行补偿。参数的 SE 值相互依赖度。

当然，这不会改变最佳拟合值，因为我们已经将Span和Plateau固定为最佳拟合值。但现在 K 的 SE 值降低了，等于 0.008605。这是有道理的。在固定跨度值和高原值的情况下，改变 K 的值对拟合优度（平方和）的影响比允许跨度值和高原值也改变以补偿K 的变化时更大。

固定其他参数时 K 的 SE 值较低，这说明 K 的不确定性依赖于其他参数。我们希望通过计算依赖度来量化这一点。

在比较两个 SE 值之前，我们必须纠正一个小问题。计算 SE 时，程序会除以自由度（df）的平方根。对于每次拟合，df 等于数据点数减去回归拟合参数数。因此，对于完全拟合，df 等于 20（数据点数）减去 3（参数数）或 17。当高原和跨度的值保持不变时，只有一个参数，因此 df=19 。由于 df 不相等，因此两个 SE 值不完全可比。其他参数固定时的 SE 值被人为地拉低了。这很容易解决。将两个参数受限时的 SE 乘以 19/17 的平方根。修正后的 SE 等于 0.00910。

现在我们可以计算依赖度了。它等于 1.0 减去两个（修正后的）SE 值之比的平方。因此，本示例中的依赖度等于 1.0-（0.0091/0.0248）2，即 0.866。从根本上说，这意味着 K 的变异中有 86.6% 是由于与其他参数的交互作用造成的。

每个参数都有明显的依赖度（除非只有两个参数）。跨度的依赖度为 0.613，高原的依赖度为 0.813。

依赖度概念的起源

关于依赖度的首次使用，似乎没有论文可以引用。依赖度的概念显然是由美国国立卫生研究院的迪克-施拉格（Dick Shrager）提出的，然后由加里-克诺特（Gary Knott）加以改进。MLAB 是第一个计算依赖度的软件，在MLAB手册中有详细解释。GraphPad Prism 简单地实现了手册中解释的方法。(我是 2007 年从 Gary Knott 的一封电子邮件中了解到这段历史的）。下面是一篇早期的论文，讨论了依赖度的基本思想，但定义有所不同（从 1 到无穷大，而不是从 0 到 1，而且数学解释也不完整。