在拟合非线性回归模型时,您可能还会对拟合优度参数值的各种变换、组合和插值感兴趣。使用模型定义对话框的 "报告变换"选项卡,可以定义这些值,以便 Prism 在报告结果时报告这些值(以及适用时的置信区间)。
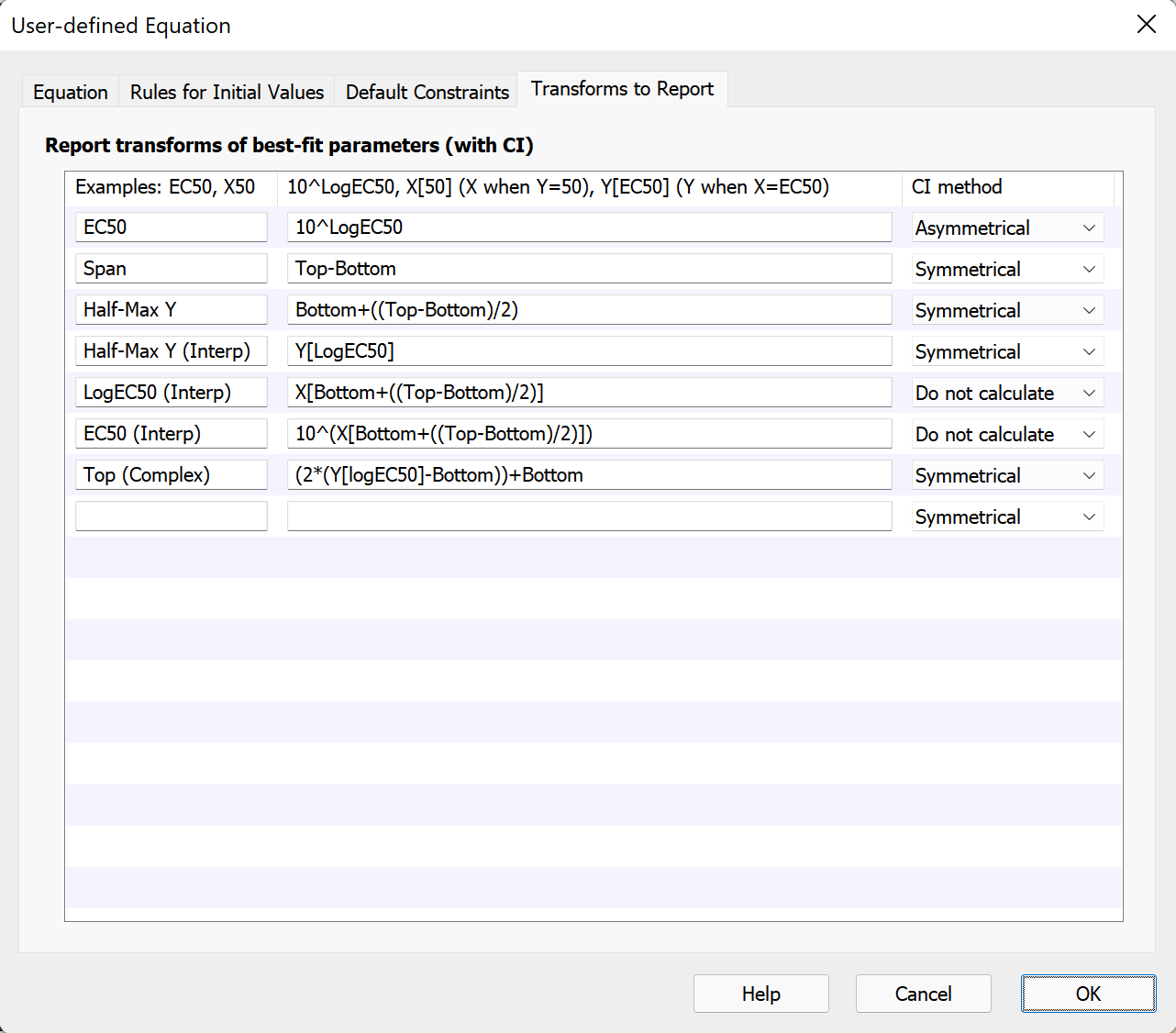
定义参数变换
为转换命名
报告转换 "对话框每行最左侧的文本框用于为该行的转换命名。该名称将显示在非线性回归结果表中,因此请选择一个您能识别的名称。
定义变换或插入值
对话框每一行的第二个文本框用于定义(方程),该定义将用于计算所需的变换或插值。请注意,定义变换时可以使用模型参数的任意组合。但是,不能将一个变换的结果作为另一个变换的输入。转换的输入只能是通过回归或标准数学运算符(对数、指数等)拟合的参数。因为这些定义是针对参数的变换而言的,所以在变换中包含 X 或 Y 是没有意义的(尽管可以 使用插值)。
本示例:您将数据拟合到一个包含参数 "logEC50"的方程中,该参数是 EC50 的对数,但您还想根据拟合优度模型参数值包含 EC50 的值和误差估计值。在左侧文本框中输入标签 "EC50",在右侧文本框中输入 "10^logEC50"(不带引号)。
本示例:您拟合了一个报告速率常数 "K"的方程数据,但您还想报告半衰期。在左侧文本框中输入标签 "半衰期",在右侧文本框中输入定义 "ln(2)/K"(不带引号)。
您还可以使用 "变换"控制来报告根据拟合优度参数值曲线计算出的数值。插值及其置信区间(如适用)将与其他变换后的参数一起出现在结果中。如果定义中包含插值,插值可以基于常量值(数字)、单个参数或多个参数的组合(函数)。请使用以下语法:
•Y[常数或参数]
当 X 为括号内输入的值时,曲线的 Y 值。任何 X 都会计算 Y 值,但只有当 X 值在 X 轴范围内时才会计算置信区间
•X[常量或参数]
当 Y 为您在括号内输入的值时,曲线的 X 值。Prism 在绘制曲线的范围内(范围选项卡)搜索输入的 Y 值,向两个方向延伸的距离等于该范围的一半。它将报告在该范围内找到的与输入的 Y 值相对应的最小 X 值,当曲线摆动导致有多个 X 值与一个 Y 值相对应时,它不会发出警报。如果 X 和 Y 都在坐标轴范围内,还会报告置信区间(如果适用)。
本示例:您拟合了一条抑制剂量反应曲线,想知道当 Y 值为 50 时的 X 值,尽管这可能不是曲线顶部和底部高原的中点(点击此处了解更多关于相对和绝对 IC50 的信息)。为此,插入值的定义如下:
•绝对 IC50 = X[50]
高级本示例:您想计算介于剂量反应曲线 "底部"和 "顶部"高原之间的 Y 值。有两种方法可以做到这一点。第一种是使用 "底部 "和 "顶部 "参数的变换:
•Half-Max Y = Bottom+((Top-Bottom)/2)
另一种方法是使用 LogEC50 参数和插值变换。由于 LogEC50 被定义为当 Y 为半最大值时 X 的值(对数刻度),因此插入以下插值可以从 LogEC50 计算出半最大值时的 Y:
•半最大值 Y (插入值) = Y[LogEC50]
下面的 "变换类型 "部分为 Prism 中可能进行的各种变换提供了更多本例。
选择置信区间类型
在每一行上都有一个下拉菜单,您可以指定所定义的变换要报告的置信区间类型。这些选项包括
•对称
•不对称
•不计算
这里的选择可能有点复杂,因为每一行的可用选项将依赖于该行的变换定义,计算结果也将 依赖于非线性回归参数对话框置信区间选项卡中关于如何报告模型参数置信区间的选择。
由于 Prism 允许包含模型参数和插入值任意组合的变换,因此该下拉菜单中的特异性选项将 依赖于所定义的变换类型(更多信息请参阅下文 "变换类型 "部分)。
我们的建议如果有 "非对称"选项,请选择 "非对称";否则请选择 "对称"。此外,在非线性回归对话框的置信区间选项卡中,我们建议始终选择不对称(剖面似然)置信区间。
本页其余部分将介绍 Prism 中可用的不同转换类型以及每种类型的可用选项
不要将变换参数的置信区间与插入值的置信区间混为一谈
尽管在 Prism 的结果表中,变换参数的置信区间和插入值的置信区间看起来是一样的,但它们实际是完全不同的。如果方程的书写方式不同,参数的变换本可以是模型中的一个参数。相比之下,插值变换代表的是曲线在指定点的预测值。插入变换的置信区间的概念与曲线的置信带的概念相同。
请注意一个潜在的混淆点。插值变换的置信区间与模型参数的简单变换在结果的同一章节中报告。该部分的标题依赖于在非线性回归参数对话框的置信区间选项卡上选择的置信区间方法:不对称(剖面似然)CI 或对称(渐近、Wald)CI。但是,插值变换的置信区间是使用与置信带有关的方法计算的,与计算参数置信度的方法无关(尽管它是在标有置信区间的部分)。
还要注意的是,剖面似然置信区间的概念不能应用于多个参数的变换。事实上,如果选择了该选项,就不会报告多参数变换的置信区间。
大多数情况下,Prism 会自动提供最合理的置信区间(如果可以计算的话),置信区间选项可以忽略。这些选项看似简单,但背后却蕴含着大量的数学知识。只有当你对这些 CI 计算的特异性非常感兴趣时,才会继续阅读下去。有了这些信息,下面的 "转换类型 "部分总结了每种转换类型的不同选项。
转换类型
有关任何特定类型变换的详细信息,请参见下面相应的章节。本图表提供了以下详细信息的快速概览:
|
置信区间法(来自非线性回归参数对话框的置信选项卡) |
||||
对称(渐近)近似 CI |
非对称(剖面似然)CI |
||||
置信区间法(从变换到报告选项卡) |
置信区间法(从变换到报告选项卡) |
||||
对称 |
非对称 |
对称 |
非对称 |
||
无插入值 |
单一参数的变换 |
对称渐近 CI |
变换渐近 CI |
变换剖面似然 CI |
变换剖面似然 CI |
多参数变换 |
对称渐近 CI |
不适用(无法在对话框中选择) |
未报告 CI(无法准确计算 CI) |
不适用(无法在对话框中选择) |
|
从 X 插入 Y 值 |
简单插值,无附加参数 |
对称渐近 CI |
变换渐近 CI |
对称渐近 CI |
变换渐近 CI |
复杂插值,无附加参数 |
对称渐近 CI |
变换渐近 CI |
对称渐近 CI |
变换渐近 CI |
|
插入值,带附加参数 |
对称渐近 CI |
不适用(无法在对话框中选择) |
对称渐近 CI |
不适用(无法在对话框中选择) |
|
从 Y 插入 X 插值 |
简单插入,无附加参数 |
不适用(无法在对话框中选择) |
变换渐近 CI |
不适用(无法在对话框中选择) |
变换渐近 CI |
复杂插值,无附加参数 |
不适用(无法在对话框中选择) |
不适用(无法在对话框中选择) |
不适用(无法在对话框中选择) |
不适用(无法在对话框中选择) |
|
插入插值,有附加参数 |
不适用(无法在对话框中选择) |
不适用(无法在对话框中选择) |
不适用(无法在对话框中选择) |
不适用(无法在对话框中选择) |
|
关于参数变换的其他说明
•Prism 9.3 改进了这一功能。在早期版本中,只能从有限的数学运算符(和、商等)中选择组合两个参数的运算符。从 Prism 9.3 开始,您可以输入任意方程,组合任意数量的参数
•Prism 4(及更早版本)总是报告 EC50 和半衰期的不对称置信区间,但不提供在用户自定义方程中转换这些参数的选择。
•当变换只是简单地改变单位时,对称区间和 "不对称"置信区间是相同的,因此选择并不重要。当参数 "K"的变换形式为 "a*K+b"时就是这种情况
•不要将本页讨论的报告变换参数 CI 的两种选择与非线性回归分析参数对话框的置信选项卡中 指定的报告模型参数 CI 的两种方法混淆起来。
•Prism 只计算单调变换的置信区间。否则,结果将是空白。函数单调是什么意思? "单调函数是指完全不递增或不递减的函数。如果函数的一阶导数(不一定是连续导数)不改变符号,那么该函数就是单调函数"(1)。
•当 Prism 报告两个参数的差或比(等)以及标准误差和置信区间时,计算会考虑两个参数的协方差。参见本文档。
参考文献
1.Stover, Christopher. "Monotonic Function." 摘自MathWorld--A Wolfram Web Resource,由 Eric W. Weisstein 创建。https://mathworld.wolfram.com/MonotonicFunction.html。