前一节介绍了危险率（或危险函数）的概念，即在单位时间内相关事件发生的频率。如果我们想用严格的数学术语来表述，我们可以这样做：

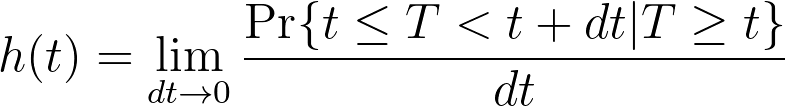
换句话说，这表明危险率（h(t)）等于相关事件在[t, t + dt]之间的某个小时间窗口内发生的概率，前提是相关事件在时间 t 之前没有发生。这被认为是瞬时危险率，因为 dt 所定义的时间窗口被认为是极小的（无限小，接近于零）。

利用贝叶斯定理并简化该表达式（此处未显示），还可以使用之前定义的pdf和生存函数来定义危险函数：

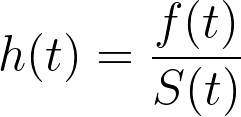
在这种形式下，危害函数可以被解读为 t 时刻的事件密度除以 t 时刻相关事件尚未发生的概率。

请再次注意--如果我们知道 pdf f(t) 的函数形式，我们就能直接计算出危害函数的形式。但是，Cox 比例风险回归并没有对这个 pdf 做任何假设，因此是一种半参数分析。