在上一节中，我们给出了生存函数的定义：

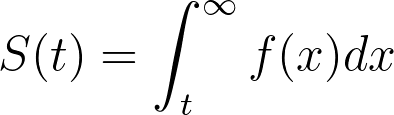
或者换句话说

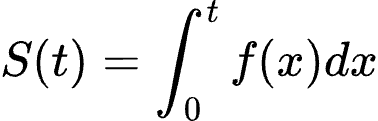
求出两边的导数，我们就可以看到：

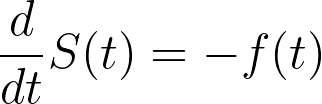
这很有用，因为函数对数的导数可以定义为

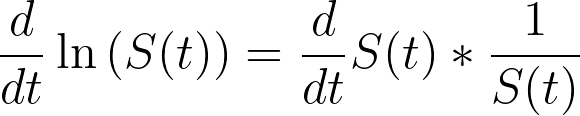
如果我们开始替换上式中的项，就可以简化这个表达式：

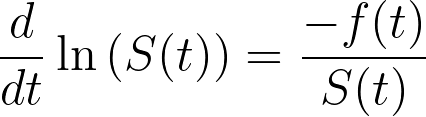
这就是我们在上一节中为危险函数提供的公式的负数：

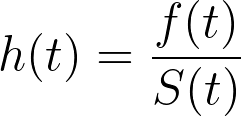
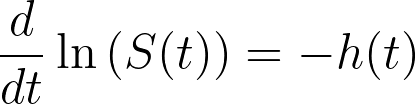
如果我们对等式左侧进行积分和指数化，就可以得出以危险率为单位的生存函数定义：

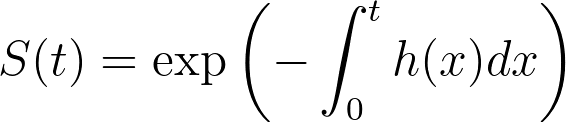
现在，让我们将上式中的积分定义为一个新概念，即累积危险函数或累积危险率，用 H(t) 表示（注意累积危险率使用大写字母 H，而瞬时危险率则使用小写字母 h）：

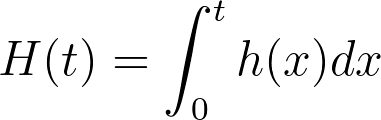
这个累积危险函数可以看作是在时间推移到 t 时，发生相关事件的总累积风险。瞬时危险率（h(t)）可以随时间增加或减少，而累积危险率只能增加或保持不变。从数学上讲，这是因为瞬时危险率必须大于或等于零。但从概念上讲，这是有道理的，因为经历相关事件的 "总累积"风险只会随着时间的推移而增加（或保持不变）。

综上所述，我们得出了使用累积危险函数的生存函数定义：

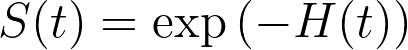
或者，等价于

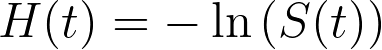
通过这两个等式，我们可以在生存函数（相关事件在 t 时间内未发生的概率）和累积危险函数（相关事件在 t 时间内的总累积风险）之间快速转换。