Cox 比例风险回归假定基线风险率（h0(t)）、预测因子变量值（xi）和参数系数（βi）之间存在如下关系：

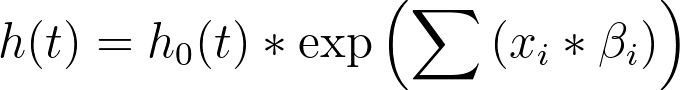
在进行 Cox 比例风险回归时，分析过程的第一步是估算模型中β（β）系数的拟合优度值。这一过程称为最大似然估计（MLE）。这项技术所涉及的数学知识远远超出了本指南的范围，但需要注意的是，根据所分析的数据以及数据中是否存在依赖度，MLE 通常使用三种不同的技术。有关这些贝塔系数的解读信息，请阅读本页的更多内容。

在收集生存数据时，代表经过时间的变异性被视为连续的，但通常是以离散的方式测量的。研究中每个人的状态每小时、每天、每周、每月等都会进行检查，为分析而记录的经过时间通常在此水平上截断。本示例中，我们可能会记录某个个体在为期 4 个月的研究中经历了 6 周的相关事件，而不是了解该个体在发生相关事件之前的确切天数（或时、分、秒等）。不过，需要注意的是，即使采用这种数据记录方法，经过的时间仍被视为连续变异性。因此，在一项研究中，经常会出现多个个体的生存时间记录相同的情况。这就是所谓的存活时间 "并列"。

当数据中没有并列关系（或并列关系很少）时，可以使用 MLE 使用 "精确"方法来确定模型中的β系数（Prism 中默认使用此方法）。但是，当事件时间中存在大量的并列关系时，这种方法的计算量就会变得非常大，这时就需要使用近似方法来计算所需的β系数值。有两种常用的近似值可以使用：

1.布雷斯罗近似法

2.埃夫隆近似法

布雷斯罗近似法是这两种方法中较早使用的一种，许多统计软件包在数据出现平局时都将其作为默认值使用。不过，埃夫隆近似法通常被认为能提供更准确的结果。当数据中存在少量并列关系时，这三种方法得出的结果应该非常相似。当并列次数较多时，Prism 会自动使用埃夫隆近似法来确定贝塔系数的值。不过，分析对话框的 "模型"选项卡上的控件允许您指定自己喜欢的方法。

本指南的后续章节将介绍如何在 Prism 中执行 Cox 比例风险回归，并指导您如何解读 Prism 从该分析中生成的结果。