在进行 Cox 比例风险回归时，Prism 会提供两个值，表示每个预测变量对风险率的影响：

•参数估计值（下文将讨论）

•风险比（另页讨论）

这两个值是彼此的简单变换，因此能提供相同的信息。如果您是 Cox 回归的新手，理解风险比可能会容易一些。

 

有关为这些参数估计和风险比计算 P 值的信息，可以在其单独的页面上找到。

 

参数估计

与 Prism 提供的其他形式的多元回归相比，Cox 比例风险回归的参数估计的解读要复杂一些。这是因为 Cox 比例风险回归所使用的模型研究的是预测变量与风险率之间的关系。以下是一般模型，以供参考：

 

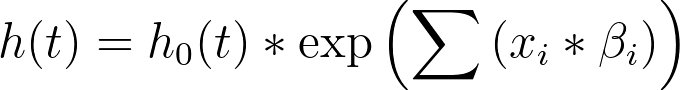
该模型的另一种表示方法是将两边除以基线危险（h0(t)），然后取自然对数，结果为：

 

这就是模型的形式，从中可以理解参数估计。本示例中的唯一预测因子是连续变量 "年龄"。如果 "年龄 "的参数估计值为 0.5，模型就会是这样：

 

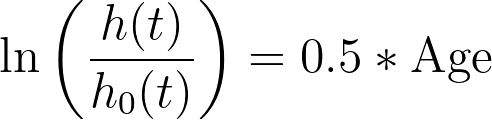
根据这个模型可以看出，如果年龄的值增加 1，对数（危险率）的值将增加二分之一。虽然这些参数估算值显示的是对数值的影响（绝对值可能难以理解），但它们确实带来了一个非常好的好处：参数估算值为正数时，表示该预测变量的增加会导致危险率的增加；参数估算值为负数时，表示该预测变量的增加会导致危险率的降低。

请记住，危险率的增加意味着发生相关事件的风险增加，而危险率的降低则意味着发生相关事件的风险降低。

 

标准误差和置信区间

参数估计，顾名思义，就是对整个人群中某些未知值的估计值。要想知道参数的真实值，唯一的方法就是收集整个人群的数据。例如，如果您想知道人类的平均身高，您可以（假设）测量每个人的身高。但是，由于实际上无法做到这一点，所以只能收集数据样本。从这个样本中，你可以计算出一个平均值，而这个平均值会因为你所选受试者的随机变异性而产生一些误差。在 Cox 比例风险回归中，Prism 报告的两个值可以让我们了解参数系数估计值的误差大小：标准误差和剖面似然置信区间。

系数的标准误差可能很难解读，但简单来说，它提供了参数估计值的精确程度。

另一种了解精确度概念的方法是置信区间。这些值说明了您对所提供的参数估计值有多大把握。置信区间的一般概念是--如果您重复大量相同的实验，并为每次重复实验构建置信区间--这些置信区间中的 95%（95% 置信区间）将包含整个群体的真实参数系数。请注意，有些软件报告的对称置信区间是直接使用上述标准误差计算出来的。Prism 实际上计算的是更精确的剖面似然置信区间。这些置信区间可以是（通常也是）围绕估计参数值的非对称置信区间。