在进行 Cox 比例风险回归时，Prism 会提供两个值，表示每个预测因子变量对风险率的影响：

•参数估计值（另页讨论）

•风险比（下面讨论）

这两个值是彼此的简单变换，因此能提供相同的信息。如果您是 Cox 回归的新手，理解风险比可能会容易一些。

 

简单版本

风险比表示给定参数对结果的"乘法效应"。如果某个参数的风险比为 2，那么该参数值每增加 1，所有时间点的风险率就会增加一倍。

 

详细版本

风险比是对之前描述过的 Cox 比例风险回归计算出的参数估计值的一种转换。如前所述，这些参数估计值（β 值）表示对数（危险率）因相应预测因子变量值的变化而变化的程度。不过，考虑危害率对数要比考虑简单的危害率复杂一些。风险比率用于表示当与此风险比率相关的预测因子变量发生变化时，风险率会发生多大的变化。

考虑一下 Cox 比例风险回归所使用的模型：

 

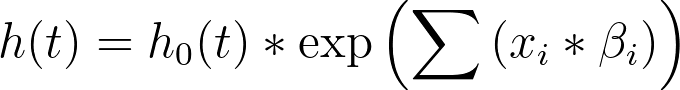
该模型的另一种表示方法是两边除以基线危险度（h0(t)）：

 

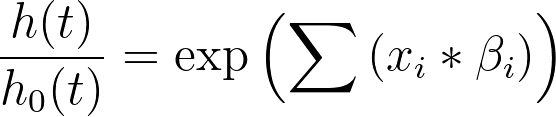
可以按以下方式展开：

 

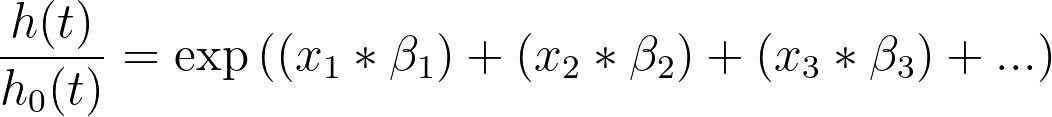
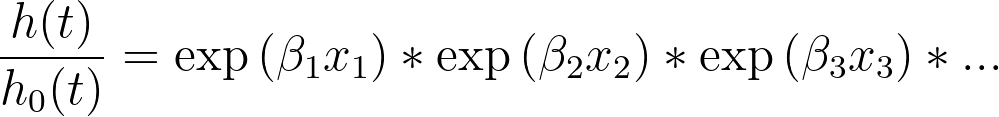
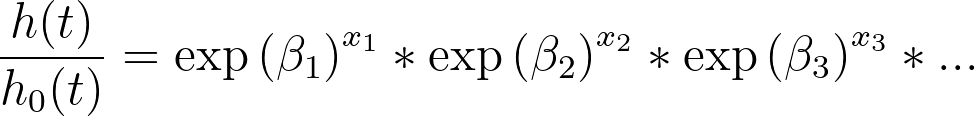
如果我们用"HR1"代替"exp(β1)"，就可以得到

 

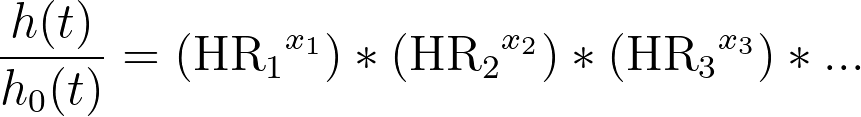
方程的这一最终形式清楚地表明了参数估计和风险变异性比率之间的关系：如果对给定预测因子变量的参数估计进行指数化，就可以得到风险比率。利用这些知识，现在可以看出这些风险比值具有如下解读：

对于给定的风险比HRi，当所有其他预测因子变量值保持不变时，xi增加一个单位对危险率的乘法效应等于风险比的值。

举个简单的本示例，假设预测因子变量"年龄（岁）"的风险比率为 2，当年龄增加一岁时，风险比将乘以 21 的值（或仅为 2）。当年龄增加两岁时，危险率将乘以 22（或 4）。风险比率提供了预测因子变量对危险率的"乘法效应"。

Prism 还为这些风险比提供置信区间。置信区间通常是被误解的统计概念，因为它们与我们的直觉所希望的不太一样。置信区间的正确解读应该是这样的："如果我们一次又一次地重复这个实验--每次都从相同的种群中选择观察值--我们期望相应的 95% 置信区间会包含真实的种群值"。