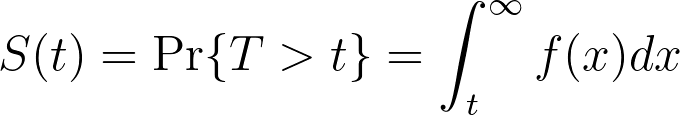在进行生存分析时，响应变量是相关事件发生前所经过的时间。这个变量是连续性的（这意味着它可以取任意多个不同的值），而且其值不能为负。我们将这个变量称为 T（大写 T 表示它是时间经过的随机变异性变量，其值是未知的。相比之下，特异性时间点将用小写 t 表示）。虽然 T 的值是未知的，但可以用一个称为 f(t)的概率密度函数（pdf）和一个称为 F(t)的累积分布函数（cdf）来定义这个变异性变量。

直接解读 pdf 一开始可能会让人有些困惑，这也超出了我们在本指南中要介绍的范围。不过，在我们继续讨论之前，有几个关于 pdf 的重要事实需要注意：

1.对于所有 t 值，f(t) 的值都是正的（大于或等于零

2.对于所有可能的T值，f(t) 曲线下的面积都等于 1

3.pdf 和 cdf 之间的关系为

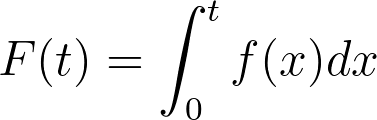
利用这些关于 pdf 和 cdf 的事实，我们可以对 F(t) 作出相对容易理解的解读：它是相关事件在时间 t（包括 t）之前发生的概率：

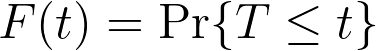
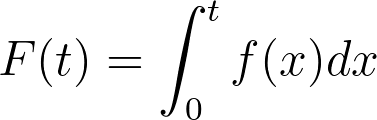
换句话说，F(t) 给出了观察到的经过时间 T 小于表达式中正在评估的特异性时间 t 的概率。然而在生存分析中，我们通常对事件在特异性时间之前发生的概率不感兴趣。相反，我们想知道事件在特异性时间之前没有发生的概率。我们可以利用前面介绍的有关 pdf 和 cdf 的一些事实来给出这种数学形式。

我们知道，pdf 在所有 t 值上的曲线下面积等于 1：

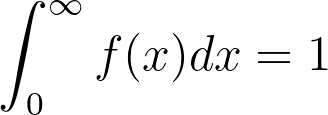
如果我们知道 cdf 是事件在 t 时发生的概率，那么 cdf 的补码一定是事件在 t 时未发生的概率，因此我们可以建立以下关系：

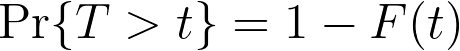
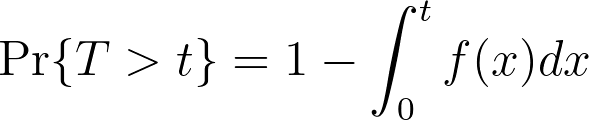
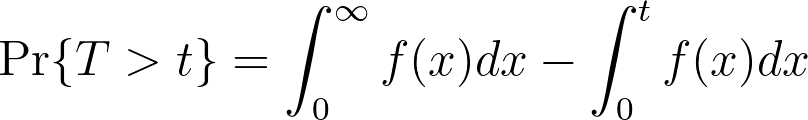
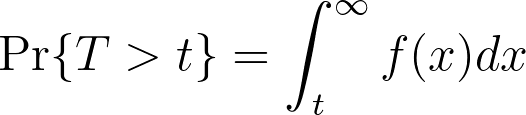
这就是所谓的生存函数，或 S(t)，它给出了相关事件在经过时间 t 时尚未发生的概率。