不要忽略置信区间
在大多数情况下,非线性回归的全部意义在于确定模型中参数的拟合优度值。置信区间可以告诉您确定这些值的严密程度。如果置信区间非常宽,说明您的数据没有很好地定义该参数。置信区间是根据参数的标准误差计算出来的。
标准误差和置信区间的准确度如何?
Prism(以及几乎所有其他非线性回归程序)报告的渐近或近似标准误差基于一些数学简化。计算时假定方程是线性的,但也适用于非线性方程。这种简化意味着区间可能过于乐观。
Prism 还允许您选择报告不对称置信区间(剖面似然区间),这些区间更准确,但计算时间更长。
Prism 有时会报告 "非常宽",而不是置信区间
如果您看到的是 "非常宽 "而不是置信区间,您也可能会在结果表的顶部看到"模糊"短语。这意味着数据没有明确定义参数。许多参数集生成的曲线同样能很好地拟合数据。曲线可能拟合度很高,使其在艺术上或插入未知数时很有用,但不能依赖拟合度最好的参数值。另外,依赖度选项卡上所选的选项,您还可能看到被识别为 "不稳定 "的特异性参数。点击此处了解有关不稳定参数的更多信息。
Prism 什么时候会将 "无穷大"报告为置信限?
当模型和数据无法定义置信上限时,Prism 会报告置信上限为无穷大。如果您的目标是 95% 的置信水平,那么无论算法将置信水平设得多大,当置信水平小于 95% 时,Prism 都会报告置信上限为无穷大。
同样,当模型和数据无法定义置信下限时,Prism 也会报告 "无限"。
当您看到置信限为无穷大(或-无穷大)时,您可以得出结论:您的数据根本没有很好地定义模型中的参数。本示例中的一个例子是,如果您正在拟合一条不对称("五参数")的 log(剂量)反应曲线,而不对称参数的置信限为无穷大。当您的数据形成对称的对数(剂量)-反应曲线时,数据中没有定义不对称参数的信息,就会出现这种情况。
Prism 何时将"??? "报告为置信限?
当计算中断,无法计算置信限时,Prism 会将"??"报告为置信限。与 Prism 7 相比,Prism 8 中的更改减少了这种情况的发生。
为什么计算会中断?原因有几个。
•可以想象,问题可能是由于数据超大或数值太小造成的。如果您的所有数据看起来都像 1.23e-45 或 1.23e45,请尝试转换为不同的单位,这样数值就不会大得惊人或小得惊人。这样做可能会有帮助,让 Prism 对置信区间进行微调。
•当模型方程从根本上难以拟合,以及数据根本无法很好地定义模型时,Prism 会报告?这可能是因为数值太少、在 X 值的重要范围内没有数值、散点太多等。即使 Prism 无法解释为什么会报告"......",您也可以得出结论:在这些数据和模型的条件下,没有办法计算出一个合理的、简短的、有用的置信区间。
转换参数的置信区间
除了报告模型中每个参数的置信区间外,Prism 还可以报告这些参数变换后的置信区间。例如,当您拟合指数模型以确定速率常数时,Prism 也会拟合时间常数 tau,它是速率常数的倒数。
当您编写自己的方程或克隆现有方程时,可以选择两种方法来计算每个转换参数的置信区间。如果选择内置方程,Prism 总是会报告转换参数的不对称置信区间。
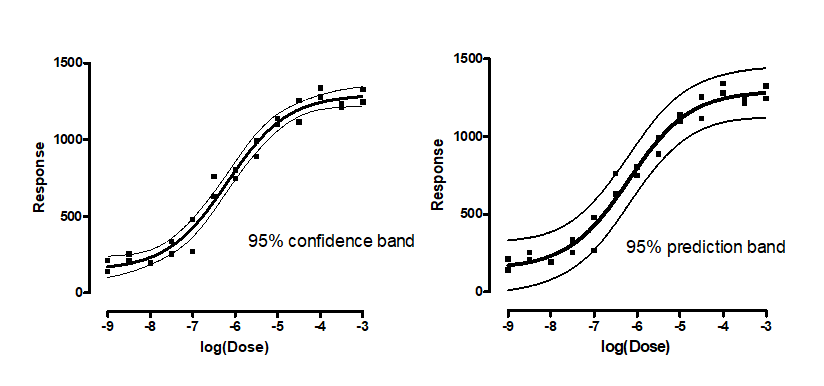
不要混淆置信区间和置信带
置信区间和置信带很容易混淆。请在 "置信度"选项卡上同时选择两者。
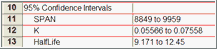
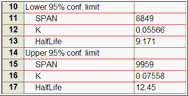
95% 置信区间告诉您 Prism 如何精确地找到特定参数的拟合优度值。这是一个以拟合优度值为中心的数值范围。Prism 可以用两种格式显示该范围:
|
|
95%置信带包围了您可以 95% 确定包含真实曲线的区域。它能让你直观地感受到你的数据在多大程度上定义了拟合优度曲线。它与 95%预测带密切相关,95%预测带包含了您期望包含 95% 未来数据点的区域。这既包括曲线真实位置的不确定性(由置信带包围),也考虑了曲线周围数据的分散性。因此,预测带总是比置信带宽。