1.创建列表

在欢迎或新建表对话框中，选择列选项卡。

2.输入 P 值

在 A 列中输入在其他地方计算出的 P 值。

每个值都必须是 P 值（介于 0.0 和 1.0 之间）。不能输入"<0.0001 "或 "ns "或 "**"。输入的每个 P 值都必须是十进制分数。

可选择在每个 P 值旁边输入一列标题，以标识相应的比较。这样会更容易理解结果。如果不输入行标题，Prism 将使用原始行号来标注结果。

这种分析通常用于数百或数千个 P 值，但也可用于任何数量的 P 值。

3.选择分析

单击 "分析"（Analyze），在 "列分析"（Column analyses）列表中查找，然后选择 "分析一组 P 值"（Analyze a stack of P values）。

 

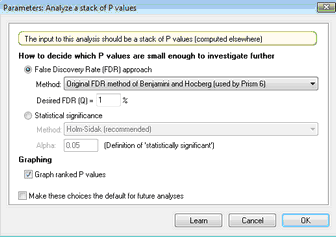
从两种一般方法中选择一种：控制 比较族的 错误发现率(FDR) 或控制 I 类错误率。然后选择您希望 Prism 使用的实际方法。

控制错误发现率 (FDR)

从三种方法中选择一种来决定哪些 P 值足够小，可以标记为 "发现"。我们推荐使用 Benjamini、Krieger 和 Yekutieli (1) 的自适应方法，因为它的检验力更强。本杰明尼和霍赫伯格（Benjamini and Hochberg）(2) 的原始 FDR 方法更为著名，但检验力较低。Benjamini 和 Yekutieli 的方法假设较少，但检验力更弱。

还要设置 Q 值，目标是在标记为发现的比较中，假发现（假阳性）不超过 Q%。请输入百分比，而不是分数。如果您希望最多只有 5%的发现是错误的，请输入 "5"，而不是 "0.05"或 "5%"。实际上并没有标准值。如果输入较大的值，更多的比较将被标记为发现，但其中更多的将是错误发现。

统计学显著性（控制比较族的 I 类错误率）

选择 Prism 如何校正多重比较。我们建议使用检验力最强的Holm-Šídák 方法。其他方法有Bonferroni-Dunn或Bonferroni-Šídák 方法。 我们所说的 Bonferroni-Dunn方法通常简称为Bonferroni。我们称之为 Bonferroni-Šídák 的方法通常简称为 Šídák。这两种方法非常相似。Bonferroni-Šídák方法的检验力更强一些，但不太被广泛理解。

设置适用于整个 P 值系列的 alpha 值。然后，Prism 会决定哪些 P 值足够小，以便在校正多重比较后将相关比较定为 "统计学显著"。输入分数，而不是百分比。 如果您希望零假设下 5%的比较被错误地标记为 "显著"，请输入 0.05，而不是 5。如果输入更大的值，更多的比较将被标记为 "显著"，但其中更多的将是假阳性。对于统计学显著性，在进行一次或几次比较时，α 通常设置为 0.05。但在进行多次比较时，您可能需要输入更大的值。

绘制图表

如果您想查看 P 值等级与 P 值的对比图，请选中该选项。这是直观显示 P 值分布的常用方法。

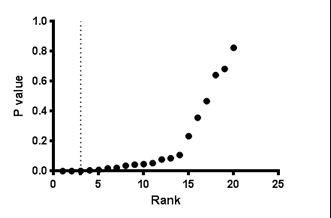
参考文献

1.Benjamini, Y., Krieger, A. M. & Yekutieli, D.Adaptive linear step-up procedures that control the false discovery rate.Biometrika 93, 491-507 (2006).

2.Benjamini, Y. & Hochberg, Y. Controlling the false discovery rate: a practical and powerful approach to multiple testing.皇家统计学会期刊》。B 系列（方法论）289-300（1995 年）。

3.Benjamini, Y., & Yekutieli, D. (2001).依赖度下多重检验中错误发现率的控制。统计年鉴》，1165-1188。