有些程序会在非线性回归结果中报告卡方检验值。而 Prism 不会。本页解释了卡方检验值的作用以及我们不报告卡方检验值的原因。

平方和是否过高？

非线性回归使数据点与曲线之间的垂直距离平方和最小。但如何解读平方和（简称 SS）呢？其实不能，因为它依赖于你收集的数据点的数量和你用来表示 Y 的单位。

卡方检验法是将观察到的曲线周围点的散度（SS）与您根据理论预期看到的实验散度量进行比较。具体做法是使用以下公式计算卡方检验：

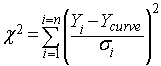
注意，分母是预测的标准偏差，而不是在此特定实验中计算的实际标准偏差。

如果您知道所有 X 值的标准偏差都是相同的，那么就可以简化为：

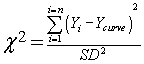
标准偏差值必须从大量数据中计算出来，因此 SD 非常准确。或者，更好的办法是，标准差可以来自理论。

如果假设重复样本按照高斯分布分散，并带有您输入的标差，而且您将数据拟合到正确的模型中，那么根据该方程计算出的卡方检验值将服从已知的卡方分布。该分布依赖于自由度，自由度等于数据点数减去参数数。 知道了卡方检验值和自由度数，就可以计算出 P 值。

如何解读一个小的 P 值？如果您非常确定散点图确实是高斯分布的，而且预测的标差是正确的，那么小 P 值就会告诉您，您的模型不正确--曲线确实没有很好地遵循数据。你应该寻找一个更好的模型。

但通常情况下，较低的 P 值只是告诉你，你对标差的预测没有你想象的那么好。很难精确确定 SD 值，所以很难解读卡方检验值。出于这个原因，Prism 没有尝试卡方检验计算。我们担心这样做的误导性大于帮助性。

替代方法

有几种方法可以回答 SS 是否过高的问题：

•可以用平方和的值来计算R2。这个值是通过比较平方和（曲线周围点的散布度量）和 Y 值的总变化（忽略 X，忽略模型）计算出来的。您期望的R2值是多少？多低的值才算低？这个问题其实不能笼统回答，因为答案依赖于你的实验系统。

•如果您收集了每个 X 值下的重复 Y 值，您可以将 SS 与根据重复间的散布预测的值进行比较。Prism 将此称为重复检验。这非常有用，但前提是您已经收集了每个 X 的重复 Y 测量值。

•您可以提出其他模型，并比较它们与数据的拟合程度。

总结

卡方检验将数据与曲线之间的实际差异与基于已知重复样本间 SD 的预期差异（假设您选择了正确的模型）进行比较。如果差异很大，那么就有证据表明您选择了错误的模型。卡方检验法的优点是可以检验单一模型的适当性，而无需提出替代模型，也无需有重复值。缺点是计算依赖于足够精确的 SD 值，而实际情况往往并非如此。

建议的替代方法是比较两个模型的拟合程度，或使用重复检验。