Prism 可以通过报告残差的标准偏差来量化拟合优度，计算方法有三种。请记住，残差是点与拟合直线或曲线的垂直距离（以 Y 为单位）。如果有 n 个数据点，回归后会有 n 个残差。

什么单位？如何解读？

所有三个值（RMSE、Sy.x 和 RSDR）的单位都与 Y 相同，都可以用大致相同的方式解读为点与直线或曲线的典型偏差。

RMSE

如果简单地取这 n 个值的标准偏差，这个值就叫做均方根误差，即 RMSE。残差的均值总是零，因此要计算 SD，只需将残差平方和相加，除以 n-1，再取平方根即可：

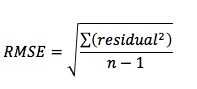
当您选中 "诊断 "选项卡中的相应选项时，Prism 会报告 RMSE，因为某些字段会用到它。但我们建议报告 Sy.x（如下）。

Sy.x 或 Se

Sy.x 的计算方法非常相似，但分母是 n-K，其中 K 是回归拟合的参数个数。n-K 的值是回归的自由度数。如果只拟合一个参数，则 RMSE 和 Sy.x 相同。如果拟合了两个或更多参数，Sy.x 会更大，是拟合优度的更好估计值。我们建议报告它而不是 RMSE。

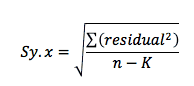
RSDR

如果选择稳健回归，Prism 会计算一个不同的值，我们称之为残差稳健标准偏差（RSDR）。这里的目标是计算一个稳健的标准偏差，而不受异常值的影响。在高斯分布中，68.27% 的值位于均值的一个标准偏差之内。因此，我们计算出这个值，并称之为 P68。事实证明，这个值稍微低估了标准差，因此 RSDR 的计算方法是将 P68 乘以 n/（n-K），其中 K 是拟合参数的个数。

 

.