虽然阿卡克方法的理论基础难以理解，但计算和理解结果却很容易。

任何模型与数据集的拟合程度，都可以用 Akaike 开发的信息准则（称为 AIC）来概括。如果接受非线性回归的通常假设（即曲线周围点的散布服从高斯分布），那么 AIC 由两个模型的平方和和自由度数的简单方程定义。这个 AIC 值本身是不可能有意义的，因为它的单位依赖于您使用的数据单位。

要比较模型，重要的是两个 AIC 值之间的差值。如果取其差值，单位就会抵消，结果就是无单位的。

对于最小二乘回归，方程为

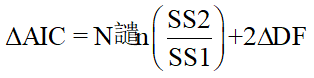
对于泊松回归，方程为：

         

逻辑回归的 AICc 等式与泊松回归的等式几乎相同（用参数个数代替等式中的自由度）。

这个等式现在有了直观的意义。与 F 检验一样，它平衡了用平方和（或泊松回归的似然比）评估的拟合优度的变化与自由度的变化（由于拟合参数数的不同）。由于模型 1 是较为简单的模型，其拟合效果几乎总是较差，因此 SS1 将大于 SS2。由于分数的对数总是负数，所以第一项也是负数。模型 1 的参数较少，因此自由度较大，使得最后一项为正。如果净结果是负数，这意味着根据参数数量的差异，平方和的差异比预期的要大，所以得出结论：更复杂的模型更有可能。

Prism 将两个 AICc 值的差值报告为简单模型的 AICc 减去复杂模型的 AICc。当较复杂（参数较多）的模型的 AICc 值较低，因此更受青睐时，Prism 会将 AICc 的差值报告为正数。当较简单模型的 AICc 较低并因此更受青睐时，Prism 会将 AICc 的差值报告为负数。

上述等式有助于您了解 AIC 的工作原理--平衡拟合优度的变化与参数数量的差异。但您不必使用该等式。只需查看各个 AIC 值，然后选择 AIC 值最小的模型。该模型最有可能是正确的。

Prism 实际上不报告 AIC，而是报告 AICc。该值包括对样本量低的修正。这个等式比较复杂，在样本量小的情况下更准确。样本量较大时，AIC 和 AICc 几乎相同。

请注意，这些计算是基于信息论的，并没有使用传统的 "假设检验 "统计范式。因此没有 P 值，没有关于 "统计学显著性 "的结论，也没有对模型的 "拒绝"。

根据 AICc 值的差异，Prism 会计算并报告每个模型正确的概率，概率总和为 100%。如果一个模型比另一个模型正确的可能性大得多（比如，1% 对 99%），你就会想选择它。如果可能性相差不大（比如 40% 对 60%），您就会知道任何一个模型都可能是正确的，因此希望收集更多的数据。这些概率是通过以下公式计算出来的，其中 Δ 是 AICc 值之间的差值。

请注意，此方法只是比较您选择的两个模型的拟合结果。有可能你没有选择的第三个模型比你选择的任何一个模型的拟合效果都要好得多。