关于风险比的主要事实

•危险度是指在单位时间内相关事件发生的频率，一般可视为生存曲线的 "斜率"。它可以衡量受试者发生相关事件的速度。

•风险比是两组间风险的比较。如果风险比为 2.0，则一组的事件发生率是另一组的两倍。

•风险比不是在任何一个时间点计算的，而是根据生存曲线中包含的所有数据计算得出的

•由于报告的风险比只有一个，因此只有在假定群体风险比在一段时间内是一致的，并且任何差异都是由于随机抽样造成的情况下，才能对其进行解读。这就是所谓的比例风险假设，也是Cox 比例风险回归的基本假设

•如果随着时间的推移，风险比并不一致，那么 Prism 报告的风险比值将不会有用。如果两条生存曲线交叉，则危险率肯定不一致（如果曲线在晚期时间点交叉，则属于例外情况，此时仍在随访的受试者很少，因此生存曲线的真实位置存在很大的不确定性）

•风险比与中位生存时间之比没有直接关系。风险比为 2.0 并不意味着中位生存时间加倍（或减半）。风险比为 2.0 意味着，与另一组受试者相比，一组受试者在给定时间点未发生相关事件，到下一个时间点发生事件的概率是另一组受试者的两倍。

•Prism 使用两种方法计算风险比及其置信区间，下面将对这两种方法进行说明。对于每种方法，Prism 都会报告风险比及其倒数。如果 A 组受试者发生相关事件的比率是 B 组受试者的两倍（即 HR=2.0），那么根据定义，B 组受试者发生相关事件的比率将是 A 组受试者的一半（HR=1/2.0=0.5）。

•关于解读风险比的其他注意事项，请参阅 Hernan (1) 和 Spruance (2) 的两篇综述。

•Duerden (6)写了一篇关于风险比的通俗易懂的好文章

两种方法的比较

Prism 报告了两种不同方法计算的风险比：logrank 和 Mantel-Haenszel。这两种方法通常会得出相同（或几乎相同）的结果。但是，当多个受试者同时经历相关事件（所谓的 "并列观察"）或风险比远离 1.0 时，结果可能会有所不同。

伯恩斯坦及其同事用这两种方法分析了模拟数据(3)。在他们的所有模拟中，比例风险假设都是真实的，两种方法产生的数值非常相似。logrank 方法（他们称之为 O/E 方法）报告的值比真实风险比更接近 1.0，尤其是当风险比较大或样本量较大时。

当存在并列关系时，这两种方法的准确性都较低。对数秩方法倾向于报告更接近 1.0 的风险比（因此当报告的风险比大于 1.0 时，报告的风险比过小，而当报告的风险比小于 1.0 时，报告的风险比过大）。相比之下，曼特尔-豪恩泽尔法报告的风险比离 1.0 更远（因此，当报告的风险比大于 1.0 时，报告的风险比过大，而当报告的风险比小于 1.0 时，报告的风险比过小）。

两个风险比相差很大意味着什么？

伯恩斯坦及其同事（3）的模拟并没有将两种方法与比例风险假设不成立的模拟数据进行比较。在另一个本示例中，比例风险假设充其量也是可疑的数据中，两种方法的风险比相差很大（相差 3 倍）。看来，曼特尔-豪恩泽尔法更重视后期时间点的危险比差异，而对数rank法对所有时间点的危险比给予同等重视。

如果用这两种方法观察到的风险比值差别很大，请思考比例风险假设是否合理。如果该假设不合理，那么用单一风险比描述整条曲线的整个概念就没有意义了。

如何计算风险比

Prism 用来报告风险比的 logrank 和 Mantel-Haenszel 方法非常相似。这两种方法在 Machin、Cheung 和 Parmar；生存分析（4）第 3 章中都有解释。

Mantel Haenszel 方法：

1.按照 Michael Vaeth 讲义第 38-40 页的解释，计算总方差 V

2.计算

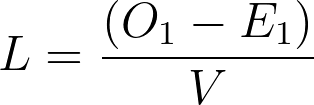
其中，O1是第 1 组事件的观察值总数，E1是第 1 组事件的期望值。如果使用另一组，您会得到相同的 L 值

3.请注意，L 是风险比的自然对数。因此

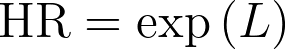
4.风险比的 95% 置信下限等于

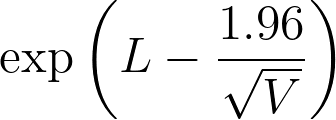
5.风险比的 95% 置信上限等于

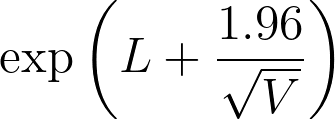
对数秩方法：

1.作为Kaplan-Meier 计算的一部分，计算每组中观察到的事件数（通常是死亡数）（Oa表示 A 组中观察到的事件数，Ob表示 B 组中观察到的事件数），以及假设生存率无差异的零假设下的预期事件数（Ea表示 A 组中的预期事件数，Eb表示 B 组中的预期事件数）。

2.风险比即为

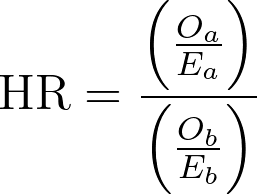
3.计算风险比的自然对数

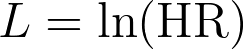
4.风险比自然对数的标准误差为

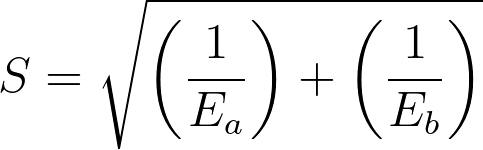
5.风险比的 95% 置信下限等于

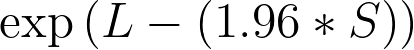
6.风险比的 95% 置信上限等于

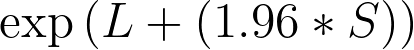
Prism 以前的版本

Prism 6 报告了使用 Mantel-Haenszel 和 logrank 方法计算的风险比。在这两种方法中，都使用风险比的自然对数（在上述计算中表示为 L）来计算 95% 置信区间的上限和下限。Prism 6 中的一个错误导致在计算对数秩方法的风险比置信限时采用了曼特尔-海恩泽尔方法。通常情况下，HRs 的差异很小，因此这个错误大多是微不足道的。只有当两个 HR 值相差很大时，它才会影响计算。在这种情况下，我们不得不怀疑这两种定义是否有很大帮助，因为在这些情况下，数据很可能根本不符合比例风险假设。7.00 (Windows) 和 7.0a (Mac) 版本修复了这个错误。

Prism 5 使用 Mantel-Haenszel 方法计算风险比及其置信区间。Prism 4 使用 logrank 方法计算风险比，但使用 Mantel-Haenszel 方法计算风险比的置信区间。结果可能不一致。在极少数情况下，Prism 4 报告的风险比可能超出所报告风险比的置信区间。

参考文献

1.M.A. Hernán.风险比，流行病学。21:13-5, 2010.

2.S.L. Spruance et all,Hazard ratio in clinical trials, Antimicrobial Agents and Chemotherapy vol. 48 (8) pp.

3.L Bernstein、J. Anderson 和 MC Pike。双治疗组临床试验中比例风险的估算》。生物计量学》（1981 年），第 37 卷（3），第 513-519 页。

4.David Machin、Yin Bun Cheung、Mahesh Parmar 著，《生存分析》：实用方法》，第 2 版，IBSN:0470870400。

5.Michael Vaeth，《临床研究中生存数据的统计分析》（2004 年）。

6.Martin Duerden,What are hazard ratios?(2009 )