中位生存时间

中位生存时间是生存概率等于 50%的时间点。需要注意一些事项：

•如果最长时间点的存活概率超过 50%，则无法计算中位存活时间。Prism 会报告中位生存时间 "未定义"。曲线的 logrank 比较比较的是整条曲线，并不比较中位生存时间。因此，即使一个或两个中位生存时间未定义，对数秩检验计算的 P 值仍然有效

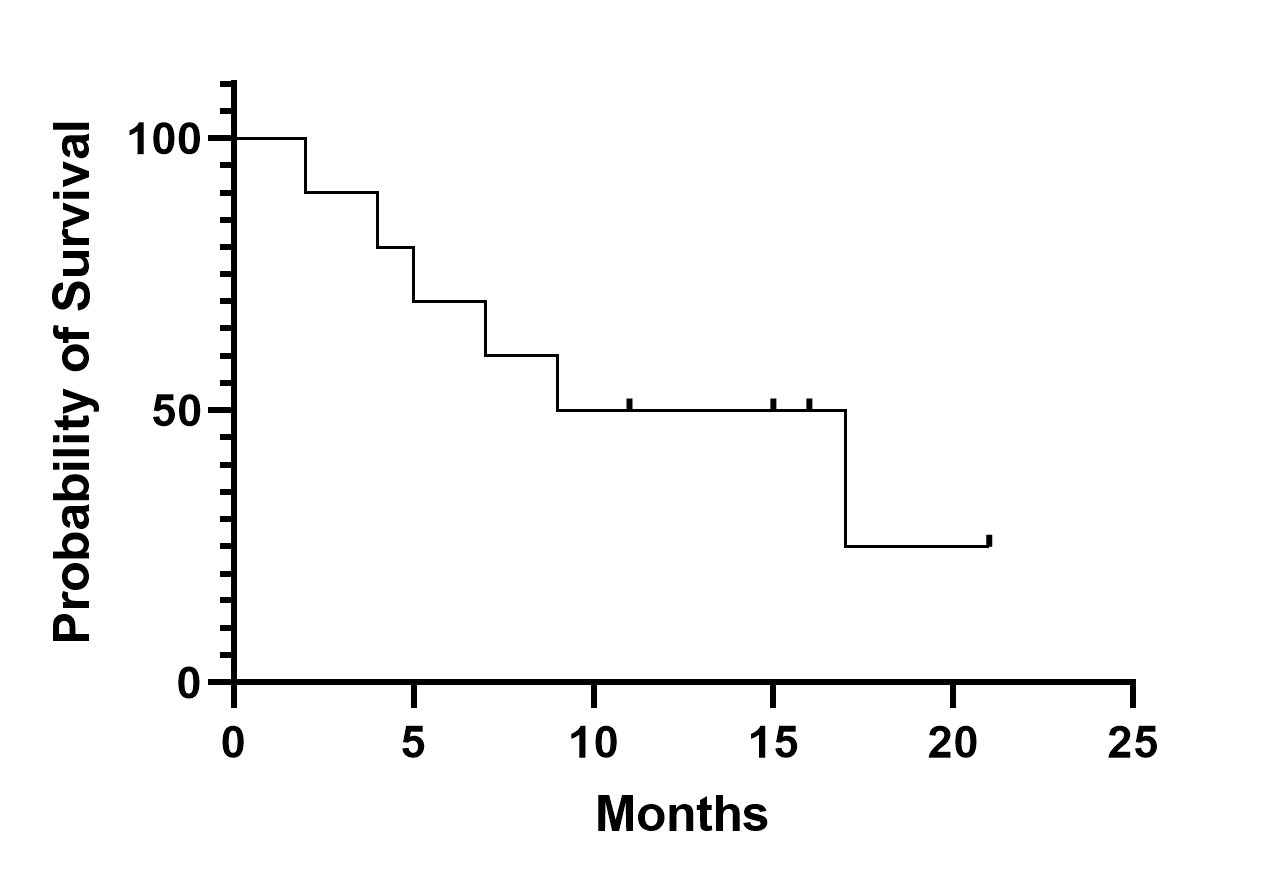
•如果生存曲线在 50% 生存时呈水平状态，则说明中位生存时间没有明确定义。在下面的生存曲线中，曲线在 9 至 17 个月之间的 Y=50% 处呈水平状态。Prism 遵循马钦的建议，报告中位生存期为这两个值的平均值，在本例中为 13 个月。

中位生存期的 95% 置信区间

在计算生存期中位数时，Prism 还会报告该估计值的 95% 置信区间（需要 Prism 10.5 或更新版本，以及具有命名用户许可证的订阅）。Brookmeyer 和 Crowley（1982 年）描述了 Prism 用来计算中位生存率 95% 置信区间的方法。由于数学细节过于复杂，本文将不再赘述。总体思路是 Prism 确定以下不等式成立的值：

其中，S(t) 是Kaplan-Meier 时间 t 的生存率估计值，g() 是一个变换函数，SE 是变换后生存率函数的标准误差。特异性地，在 Prism 中，g 使用的是互补对数-对数变换，因此该不等式的形式如下：

这里的一般想法是，该不等式成立的时间是真实中位数的可信值，而边界则代表中位数 95% 置信区间的上下限时间。请注意，下边界可能等于零，而上边界可能未定义（在 Prism 中报告为 "+无限"）。

了解更多信息（包括变换方法和标准误差计算的不同选择）：

•Talsma, P. A. (2023).使用 SAS PROC LIFETEST 估算中位生存时间及其 95% 置信区间。生物制药统计学杂志》，34（3），366-378。

•Brookmeer 和 Crowley，《生存时间中位数的置信区间》。生物统计学》（1982 年），第 38 卷（1），第 29-41 页。

•Barker 回顾了几种方法，并指出了其结果的不同之处。 Kaplan-Meier 生存估计值的平均值、中位数和置信区间--计算与应用》。The American Statistician (2009) vol. 63 (1) pp.

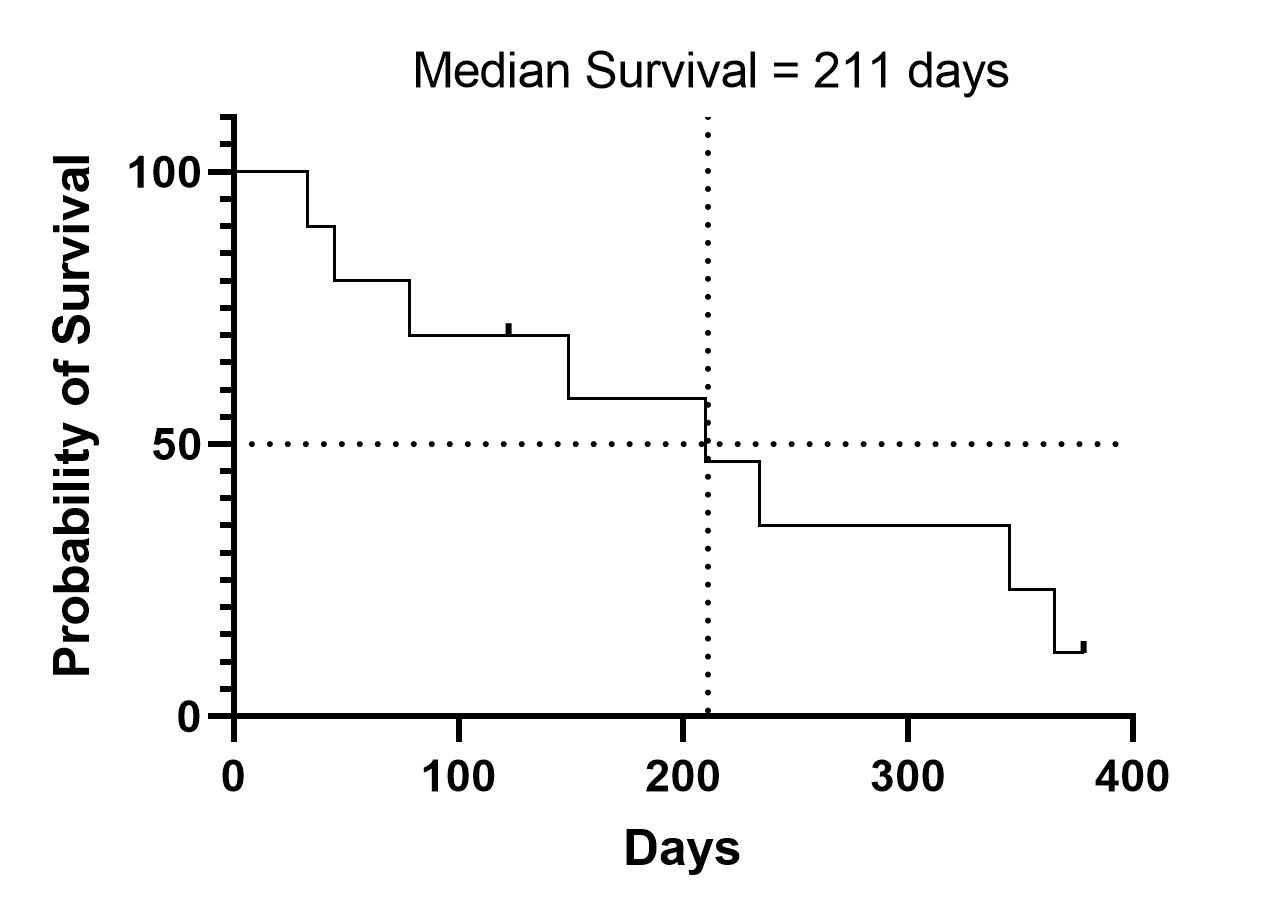
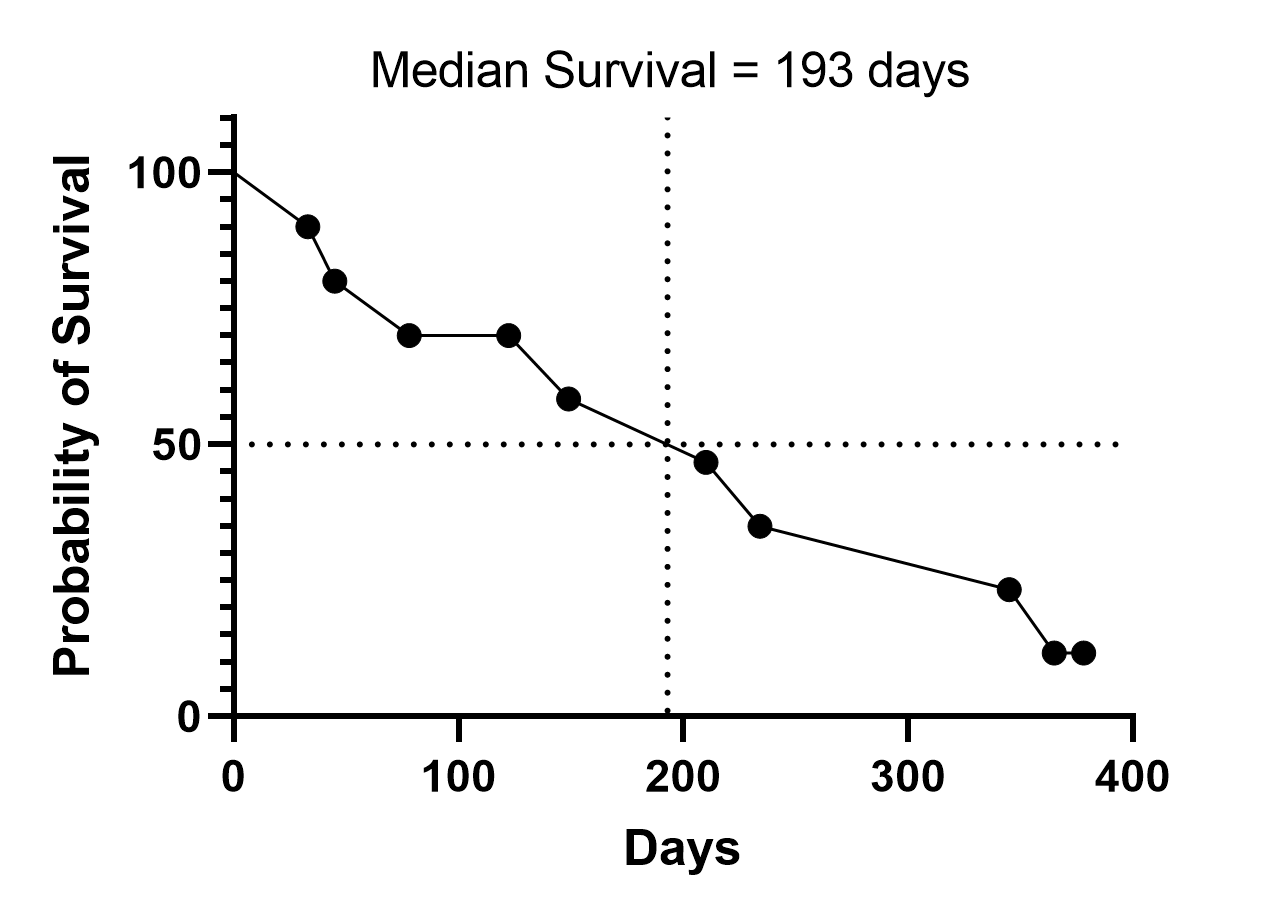
计算生存时间中位数假定采用 "stairstep"方法

Prism - 与大多数程序一样 - 将中位生存时间定义为阶梯生存曲线与 50% 生存率交叉的时间。这是对实际包含在数据集中的受试者或动物的中位生存时间的准确表述。下图左侧的示例图表显示了 Prism 如何计算存活中位数（本示例中为 211 天）。如果用点到点的直线而不是阶梯形连接存活时间，就会发现直线可能在更早的时间与 Y=50% 相交，从而得出不同的存活中位值（下图右侧示例中为 193 天）。如果要预测未来患者的中位生存期，这样做是有意义的。但 Prism 并没有这样做，因为它不是标准的