重复测量的定义
重复测量意味着数据是匹配的。下面是一些本示例:
•您对每个受试者的因变量进行多次测量,可能是在干预之前、期间和之后。
•招募受试者作为匹配组,根据年龄、种族和疾病严重程度等变异性进行匹配。
•多次进行实验室实验,每次都同时进行几种处理。由于您预计实验与实验之间会有变异性,因此您希望在分析数据时将每次实验都视为匹配组。 尽管您无意这样做,但由于外部因素(如某天比另一天更潮湿,或实验者无意中的练习效果),实验内部的反应可能比不同实验之间的反应更相似。
匹配不应基于所比较的变异性。如果您要比较三组人的血压,根据年龄或邮政编码匹配组是可以的,但根据血压匹配组是不可以的。
严格来说,重复测量一词只适用于对一个受试者反复进行治疗的情况(上述第一个示例)。另外两个本示例称为随机区组实验(每组受试者称为一个区组,在每个区组内随机分配治疗)。重复测量和随机区组实验的分析方法相同,Prism 总是使用重复测量一词。
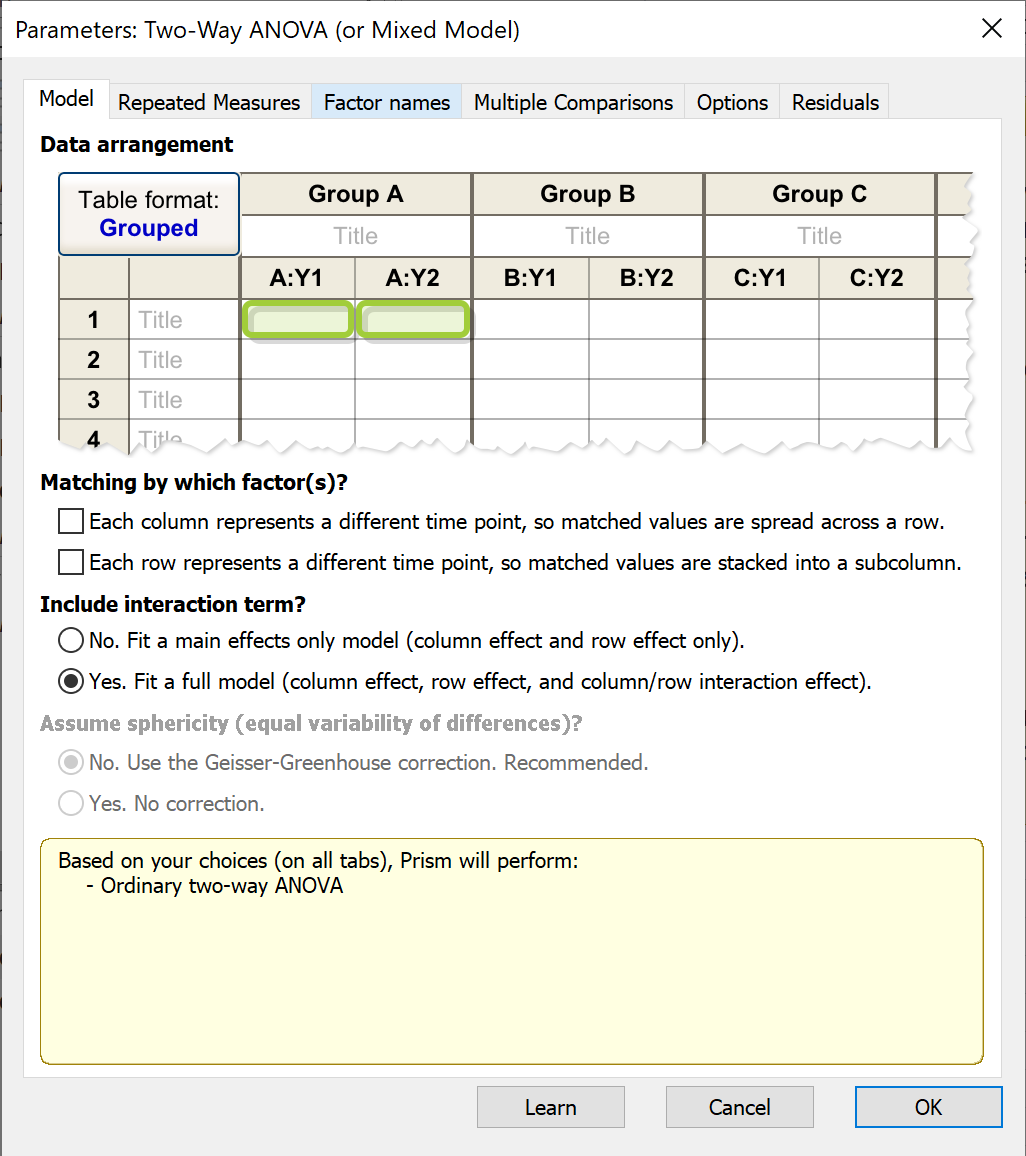
通过哪些因素进行匹配?
如果数据是匹配的,请选择两个因素中哪个是重复测量,或者两个因素都是重复测量。如果一个因素是重复测量,另一个因素不是重复测量,这种分析也称为混合效应模型方差分析。
请慎重选择,因为如果您的选择与实验设计不符,结果可能会非常具有误导性。可选项有
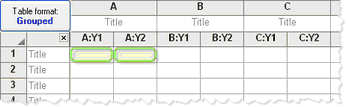
不匹配。使用常规的双向方差分析(非重复测量)。
|
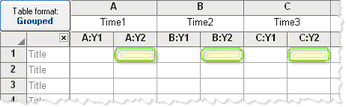
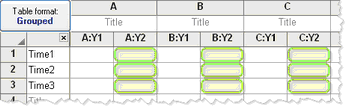
每列代表不同的重复,因此匹配值分布在一行中。
|
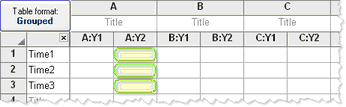
每一行代表不同的时间点,因此匹配值被堆叠到一个子列中。
|
两个因子的重复测量。
|
我们发现很多人都会想到 "重复测量",但却没有花时间仔细说明哪个因子重复或两个因子都重复。如果您的选择与实际实验设计不符,结果很可能是错误的。
包含交互作用项?
选择拟合完整模型(包括列效应、行效应和列/行交互作用效应)或仅拟合主效应(列和行效应,无交互作用)方差分析模型。知道选择其中的哪一个选项依赖于实验内是否存在交互作用,严格来说,这是一个科学决策,必须基于对实验和数据的了解。
为了更好地理解交互作用的概念,请考虑以下假设的实验设计。您对一种实验药物对血压的影响很感兴趣,因此您招募了一组男性和女性,并准备了药物和安慰剂。为了进行这项实验,您将参与者分为以下几组:
1.接受安慰剂的女性
2.接受药物治疗的女性
3.接受安慰剂的男性
4.接受药物治疗的男性
在这个实验设计中,有两个 "主效应",即治疗效应(安慰剂与药物)和性别效应(女性与 男性)。本示例显示,与服用安慰剂的人相比,服用药物的人血压较低(治疗的主效应)。您还可以预期女性的血压会比男性低(性别的主效应)。这些效应可以通过以下假设进行检验:
•对于治疗效果,您可以检验以下假设:接受安慰剂治疗的人的血压与接受治疗的人的血压相同(忽略这些人的性别差异)。
•对于性别的影响,您将检验这样一个假设,即女性的血压与男性的血压相同(忽略这些人属于哪个治疗组)。
到目前为止,这描述的是一个 "主效应 "方差分析模型,不包括交互作用项。如果一个因素(治疗)的影响依赖于第二个因素(性别)的影响,则会在模型中加入交互作用项。在上述情况中,交互作用的本示例可能是治疗会增加 男性的血压(与服用安慰剂的男性相比),而治疗会降低女性的血压(与服用安慰剂的女性相比)。换句话说,治疗效果(第一主效应)依赖于个体的性别(第二主效应)。在这种情况下,您希望加入交互作用项,并选择 "完全模型"。
还要注意的是,如果一个或多个效应组合完全缺失值,则无法使用完整模型,Prism 将仅拟合一个主效应方差分析模型。以上面的本示例为例,如果没有得到 "接受安慰剂的男性"(或任何其他单个组别)的值,Prism 将只能 拟合一个只有主效应的方差分析模型。
假设球形性?
对于双向重复测量方差分析,请选择是否假设球形性。如果不假设球形性,Prism 会使用 Greenhouse-Geisser 修正并计算ε。
球形性假设指出,处理 A 和处理 B 之间差异的方差等于处理 A 和处理 C 之间差异的方差,处理 A 和处理 C 之间差异的方差等于处理 A 和处理 D 之间差异的方差,处理 A 和处理 D 之间差异的方差等于处理 B 和处理 D 之间差异的方差......(或者,当重复测量堆叠在子列中时,处理 1 和处理 2 之间差异的方差等于处理 1 和处理 3 之间差异的方差......)。与所有统计假设一样,这一假设涉及数据的抽样群体,而不仅仅是这些特定的数据集。
请注意,如果重复测量的因子只有两个水平,那么就没有理由担心球形违背。本示例中,如果每个受试者在治疗前后都进行了测量,并且有四种不同的治疗方法,那么就没有必要担心球形性,因为重复测量因子只有两个水平(治疗前和治疗后)。如果您要求在重复测量因子只有两个水平的情况下进行 Greenhouse-Geisser 修正,结果将与您未选择该选项时的结果相同,报告的ε值将为 1.0000000。