参数估计

您将看到的第一部分结果是指定模型的回归系数（β 系数）的拟合优度值。请注意，与其他一些多元回归技术不同，Cox 比例风险回归不包含截距项 (β0)。即使在模型中强行加入截距项，它也会被基线危险（h0(t)）"吸收"。另外需要注意的是，当模型中包含变异性变量时，这些变量会被自动"虚拟编码"，从而导致除参考水平以外的每个变异性变量水平都有一个单独的参数估计。因此，我们的模型结果包括 13 个独立的贝塔系数，如下所示：

 

对这些参数估计的解读与标准多元线性回归有些不同。考虑一下本次分析的 Cox 比例风险模型：

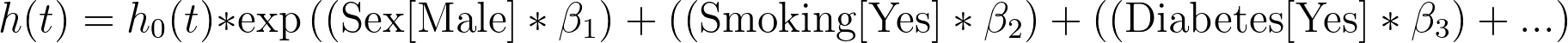
如果我们通过除以基线危险度来重新排列这个等式，就会得到以下结果：

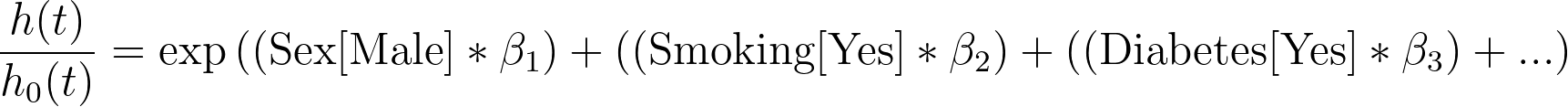
最后，如果我们对两边取自然对数，就会得到这种形式：

使用这种形式的等式，现在可以看出，等式的左侧是特定个体或群体（使用与该个体或群体相对应的特定预测变量）的风险比率比的对数，除以基线风险（表示所有预测变量设为零或其参考值时的风险比率）。这就是比例风险一词的由来，因为本分析中的模型实际上是在估算风险比率（用不同预测变量指定的组别和基线组别）。

了解了这一点，我们就可以知道，β 系数的值代表对数危险率的增加（正值）或减少（负值）。本示例中，β1（Sex[Male]）等于-0.1879。这意味着与女性相比，男性在所有时间点的对数危险率都下降了 0.1879。β6（年龄）的值为 0.04589。这意味着，年龄每增加一岁，对数危险率就会增加 0.04589。

风险比

贝塔系数的直接解读比较复杂，因为这些系数对应的是对数危险率的变化，而相对于对数尺度，一般更容易理解线性尺度上的变化。因此，结果的下一部分是风险比。

 

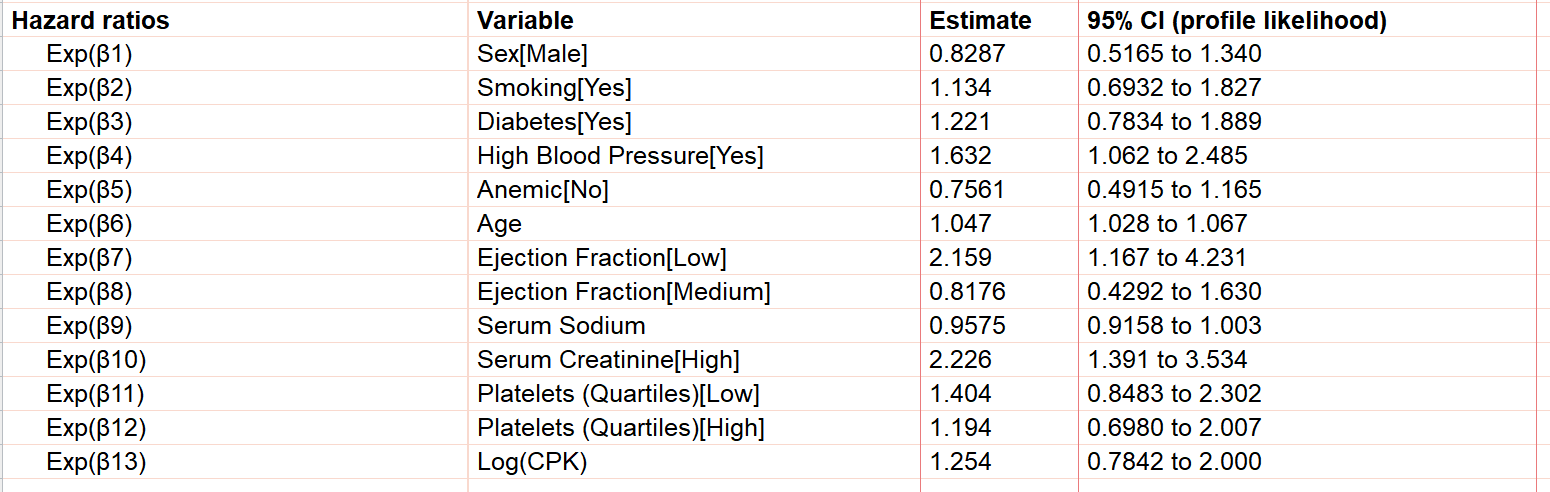
关于参数估计和风险比率之间关系的更详细讨论可以在这里找到，但从本质上讲，风险比率表示当与风险比率相关的预测因子变量增加 1 时，风险率会增加（或减少）多少倍。还是以年龄为例，我们可以看到风险比等于 1.047。这意味着参与者的年龄每增加一岁，其风险比就会增加 1.047 的倍数。从数学上讲，风险比就是简单的指数化贝塔系数（例如，年龄的风险比 1.047 相当于 exp(0.04589)，其中 0.04589 是该模型中年龄的贝塔系数）。

考虑到所有这些因素，我们可以看到，到目前为止，该模型得出的一般结论是，我们预计心脏功能差（射血分数低）、血压高和肾功能差（血清肌酐高）的老年人的危险率会升高（因此生存时间会缩短）。还要注意的是，虽然年龄的风险比看起来相对较小（本示例中年龄的风险比为 1.047，而血清肌酐高的风险比为 2.226），但这是年龄每年的影响。这意味着，年龄每增加 1 岁，危险比仅增加 1.0471= 1.047 倍，但年龄每增加 10 岁，危险比将增加 1.04710= 1.58 倍！

P 值

默认情况下，结果中不会给出参数估计的 P 值，因此这里也不会详细讨论。但是，如果您希望在分析结果的表格中包含 P 值，可以在分析对话框的选项卡中启用该选项。有关如何解读这些 P 值的更多信息，请点击此处。

模型诊断

Cox 比例风险回归的表格结果的下一部分提供了将指定模型与不包含预测变量（协变量）的模型进行比较的信息。默认情况下，这里显示的值包括每个模型的参数数和 Akaike 信息准则 (AIC) 值。其他诊断值可在分析对话框的"选项"选项卡上添加。

通过本节列出的 AIC 值，您可以快速评估分析中指定的模型是否比空（无效）模型更能拟合数据。AIC 值的计算方法有点复杂，但使用这些值来比较两个模型实际很简单：AIC 值越小表示模型拟合值越好。没有协变量的模型值为 1018，分析中指定的模型值为 960.5，我们可以确定指定的模型在描述观察数据方面做得更好。

 

数据总结

Cox 比例风险回归的表格结果页面最后一部分简单地提供了输入数据的详细摘要，包括输入数据表中的数据行数、跳过的行数以及这两个值之间的差值导致的分析中包含的观察值数。接下来，本节将报告并列（事件发生时间相同的观测值）的数量。之后，提供删剪观测值的数量和有死亡/相关事件记录的观测值的数量。根据这两个值，报告删剪观察值与事件的比率。依赖于所研究的事件，这一比率可能会有很大的不同（当事件相对不常见时，删剪观测值与事件的比率可能会很大，如本示例；当事件很常见时，比率可能会很小，因为大多数观测值都会导致事件发生）。

此外，本节还重复了删剪观察值的数量和观察值的总数，以及这两个值的比率（提供了分析中使用的删剪观察值的比例）。最后，重复计算有死亡/相关事件记录的观察值数量、参数估计总数以及这两个值的比值。一般来说，每个参数的事件数比率应在 10 左右。

 

单个值

默认情况下，Cox 比例风险回归还会生成另外两个结果选项卡。第一个是"个体值"选项卡。顾名思义，这个结果表提供了输入数据表中每个个体（行）的计算值。每个个体的经过时间，以及线性预测因子、风险比（exp[线性预测因子]）、根据生成的模型计算出的每个个体在报告的经过时间内的累积风险和累积存活率都包含在该表中。有关如何计算这些值的特异性详情，请参阅本页指南。

 

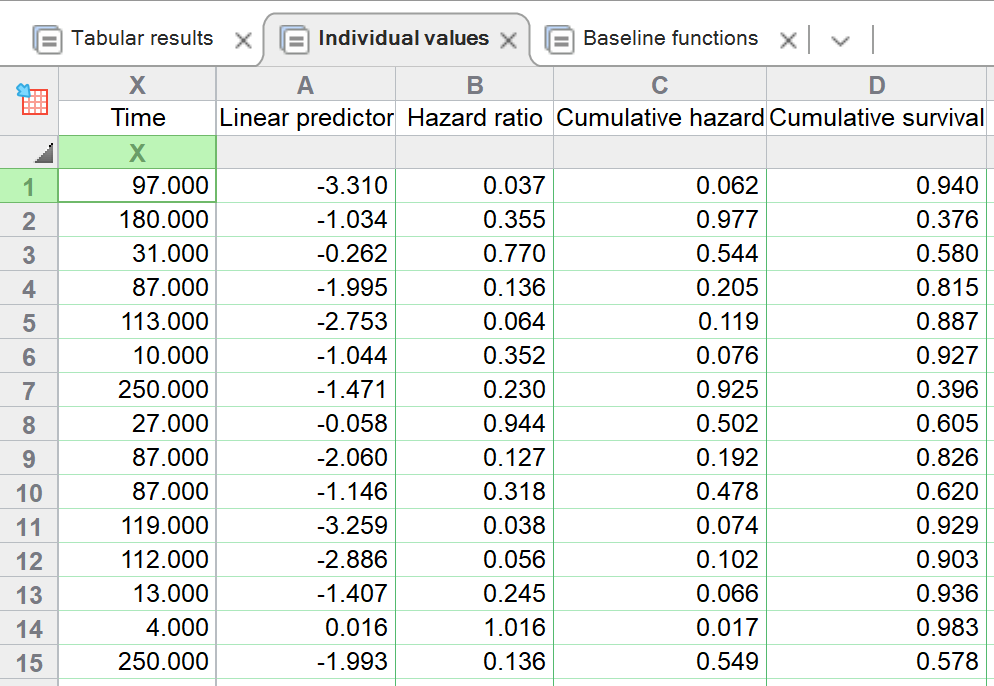
基线值

除了为输入数据表中的每个特异性观察值（行）提供估计值外，Prism 还为基线累积危害 (H0(t)) 和基线累积存活率 (S0(t)) 生成一个基线值表。与单个值表不同的是，该表包括输入数据中每个唯一时间的一行，并按这些时间值升序排序。

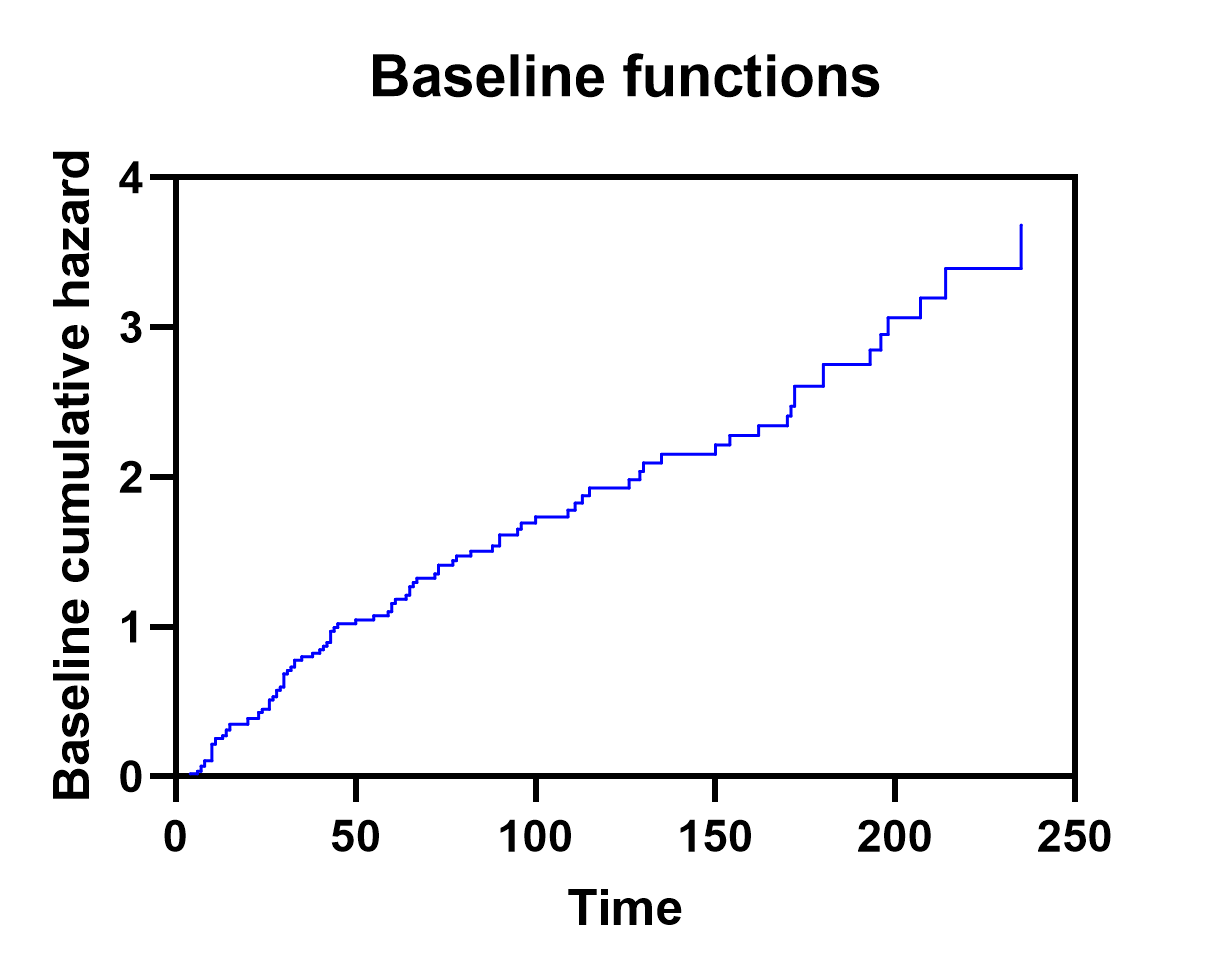
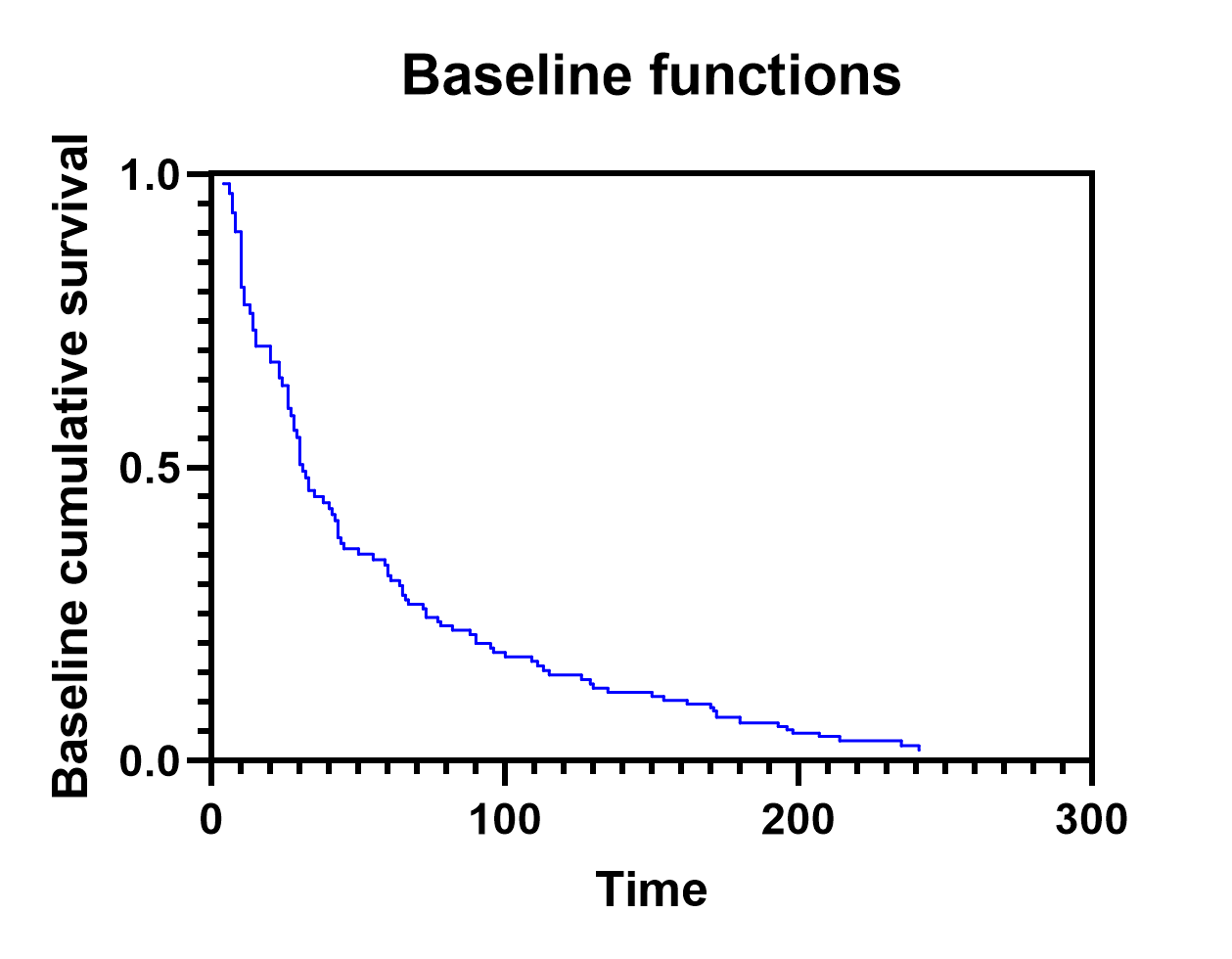
基线累积危险度和基线累积生存率的计算方法将在另一页中介绍，但需要注意的是，该表用于生成基线值图表，可以设置为显示基线累积危险度或基线累积生存率（本分析的两个示例均如下图所示）。

重要的是，这些基线图随后可用于利用每个预测因子变量的参数估计（或风险比）为指定人群构建估计生存/风险曲线。

 

残差图

默认情况下，Prism 会生成三种不同的残差图：

•缩放舍恩费尔德残差与时间/行顺序的关系图

•离差残差与线性预测因子/HR

•偏差残差 vs 协变量

每种残差图都可用于检查模型拟合的不同方面。

 

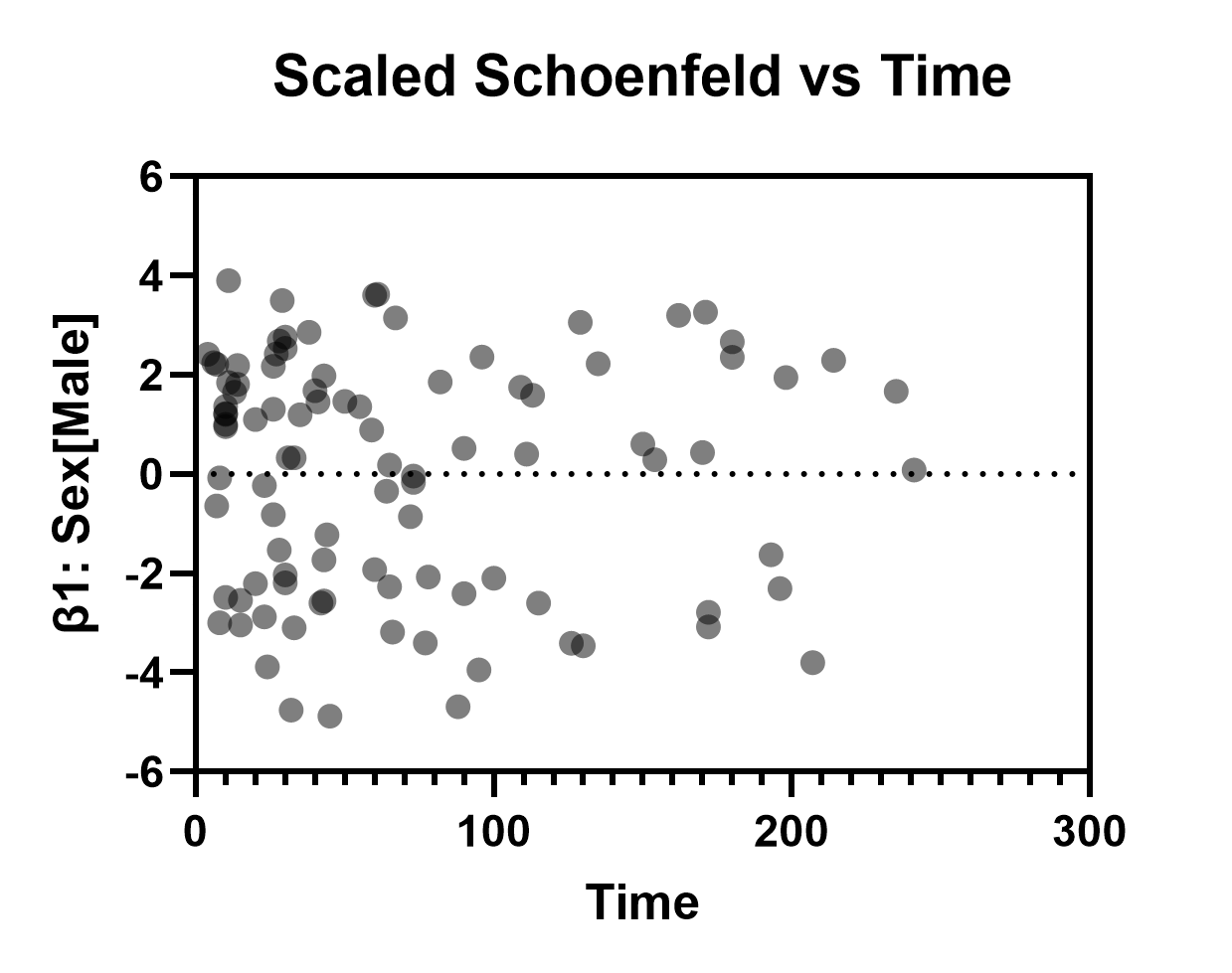
缩放舍恩费尔德残差 vs 时间/行序

该图的主要用途是检验指定模型的比例风险假设。为模型中的每个参数（在我们的例子中为 β1 至 β13）生成一组缩放舍恩费尔德残差。通过在 Y 轴上绘制这些残差图与在 X 轴上绘制时间的对比图，我们期望所绘制的数据没有明显的趋势。可以在同一张图表上检查每组不同的残差（使用设置图表格式对话框更改 Y 轴上绘制的变量），这些残差中的任何强烈趋势都表明可能违反了比例风险假设。在我们的案例中，这一假设似乎是成立的（下面给出了 β1:Sex[Male] 和 β6:Age 的本示例）。

 

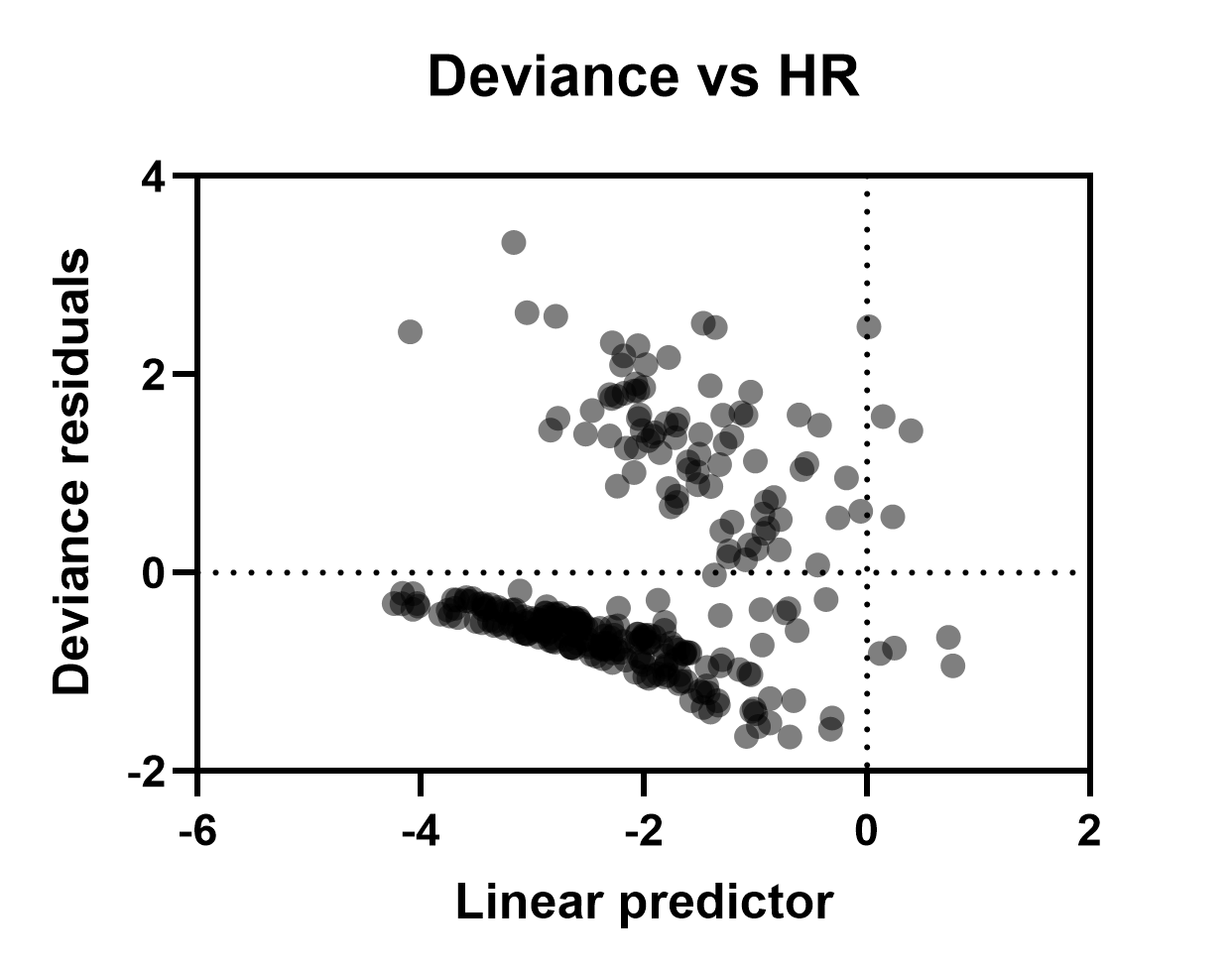
离差残差与线性预测因子/HR

该残差图可用来检查数据是否存在异常值。这些残差将以零为中心。极大或极小的值代表数据中潜在的异常值。这些点表示受试者经历相关事件的时间比模型预测的早得多（极大的正残差）或比模型预测的晚得多（极大的负残差）。使用"设置图表格式"对话框（在图表区域双击打开），可以在 X 轴上绘制每个观察值的线性预测因子或风险比（在结果的"个人值"选项卡上提供的值）。这两者之间唯一的区别是缩放（因为风险比是指数化的线性预测因子）。请注意，下图左下方区域的大密度点群是由于数据集中删剪观测值的比例较高所致。根据定义，删剪观测值必须具有负偏离残差（基于用于计算残差的数学公式，此处未显示）。直觉上，这是有道理的。被删剪的观测值没有观测到的事件时间。因此，这些观察到的事件时间不可能早于模型预测的时间（模型偏差残差为正的要求）。因此，所有删剪观测值的偏差残差必须为负。

 

偏差残差与协变量

这些残差图用于检验每个协变量的线性假设。在绘制模型偏差残差与每个协变量的关系图时，预计这些残差将大致以零为中心。这些图形中的趋势可能表明所选协变量的线性假设已被违反。请注意，目前 Prism 只能在这些图表的 X 轴上显示连续预测变量（协变量）。我们的模型变异性残差与年龄的关系图如下所示，没有显示明显的趋势，说明没有违反该预测因子的线性假设。

 

估计生存图

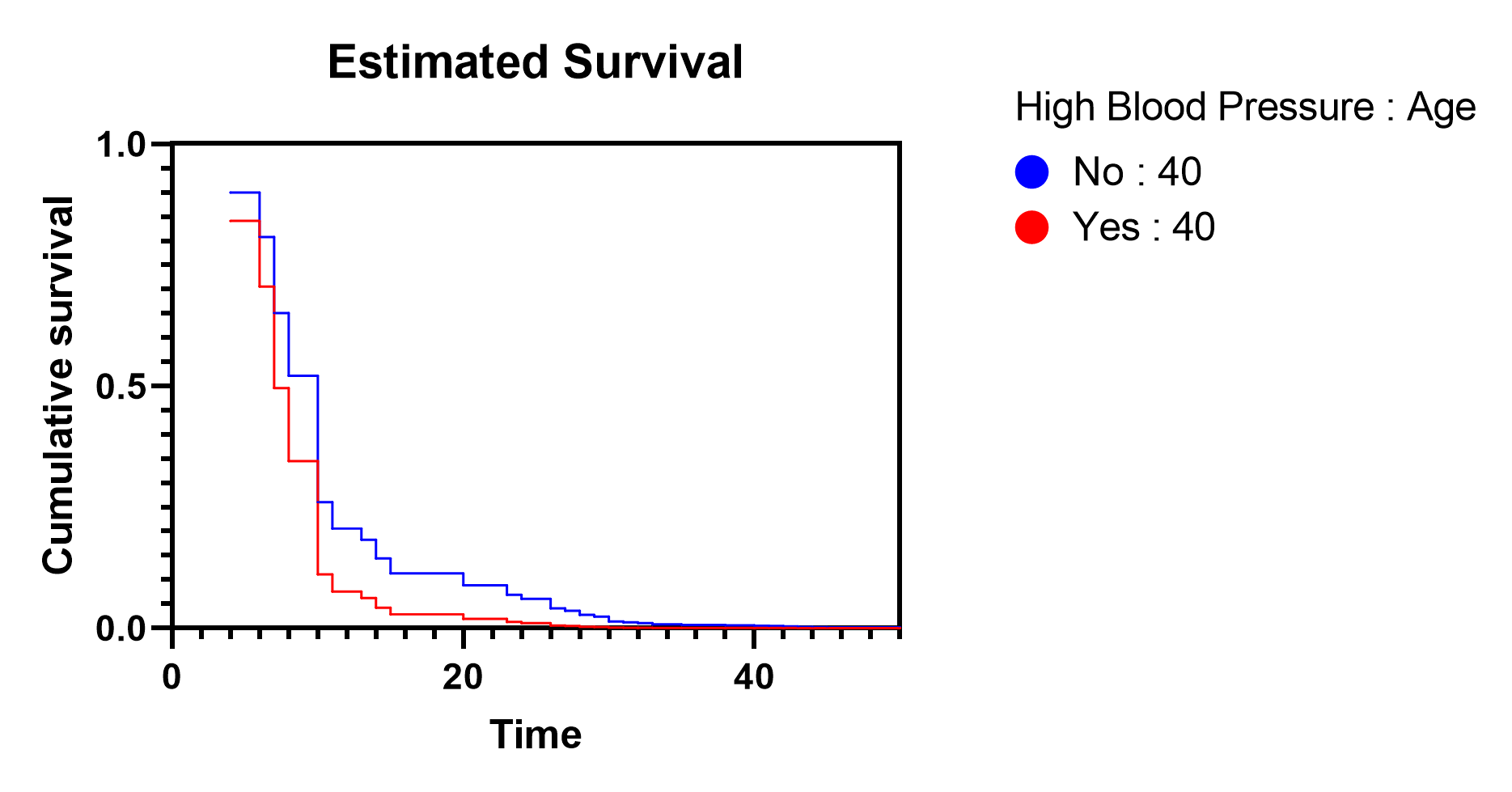
分析生成的最后一个图形包含我们在分析参数对话框的"图形"选项卡上指定的各组的估计生存曲线。使用该选项卡上的选项，我们选择了高血压（同时选择了"是"和"否"值）和年龄（值为 40）这两个变异性变量。Prism 利用这些信息和基线生存曲线（本页讨论）生成了两个人群的估计生存曲线：

•血压高且年龄为 40 岁的人群

•血压低且年龄为 40 岁的人群

Prism 生成的曲线图向我们展示了一些重要的概念。首先，我们看到高血压患者的生存概率低于非高血压患者。这与我们之前看到的同一预测因子变量的参数估计值（和风险比率）相吻合。参数估计值为正（β4 = 0.490），导致危险比大于 1（HR=1.632），这表明与无高血压者相比，高血压者的风险更高（生存概率更低）。

这些估计的生存曲线所展示的另一个非常重要的概念是比例风险假设。这一假设指出，每个人的风险都与某个基线风险成比例。这一假设可以通过一系列不同年龄值的估计生存曲线直观地显示出来。下图包括基线生存曲线以及代表不同年龄值的五条不同曲线。

 

可以看出，每条生存曲线都采用了相同的一般形状，任何特定时间的生存概率特异性值都与该时间点的基线生存概率成正比。