在详细了解 Prism 报告的 Cox 比例风险残差值之前，必须指出这些残差并不是传统意义上的残差。对于线性回归（多元线性回归或简单线性回归）和非线性回归，残差代表观察值与模型估计值（特异性地说是模型对该观察值预测的平均值）之间的差值。

遗憾的是，Cox 比例风险回归中的残差概念并没有采用相同的定义。相反，在 Cox 比例风险回归中作为残差呈现的值只是提出并用于回答 Cox 回归中许多相同问题的度量指标，而在其他类型的回归中，经典残差也是用于回答这些问题的。下面的章节将对 Prism 作为 Cox 比例风险回归的一部分提供的每种残差图进行简要说明。

比例风险假设是否有效？

这个问题是 Cox 比例风险回归分析的核心问题（就在名字里！）。一般的想法是，人群中每个个体的相关事件的发生都受一个单一的基本基线危险函数的支配，而每个个体在任何时间点的特异性危险率都只是这个基线危险率的缩放版本。从贝塔系数估计值的角度来思考这一假设的另一种方法。要使比例风险假设成立，这些参数估计值必须与时间相关恒定。

为了检验这一假设，Prism 提供了两种不同的图形。第一种是缩放 Schoenfeld 残差与时间/行顺序的关系图。重要的是，模型中的每个参数都有一组缩放的舍恩费尔德残差。这将舍恩费尔德残差与 Prism 为 Cox 比例风险回归提供的其他残差类型（输入数据中的每个观测值都有一个残差）区分开来。其原理是，当对给定参数进行缩放的舍恩费尔德残差图与时间相对应时，它们应该以一条水平线为中心，即以 0 为中心。如果这些残差存在趋势，则可能是参数估计相对于时间存在一定的时间依赖度（从而违反了分析的比例风险假设）。

另一种可用于检验比例风险假设的图表是对数减对数图（绘制输入数据中定义的多个组的 Ln(-Ln(S(t))）与时间的关系图。使用参数对话框中的对照组，Prism 将允许您指定不同的组别（由预测因子值定义）来绘制估计的生存曲线。在绘制这些生存曲线的负自然对数（Ln(-Ln(S(t))))）与时间的对数值时，每组数值应大致为一条直线。此外，如果比例风险假设是正确的，那么对于任何给定的组别来说，这些直线都应该是平行的。因此，如果这些直线交叉，就很有可能违反了比例风险假设。

观测值中是否存在异常值？

可以将离差残差和马丁格尔残差与线性预测因子（XB）或观测值的风险比进行对比绘制，而将舍恩费尔德残差与时间或行序进行对比绘制，以检查输入数据中是否存在异常值。

模型偏差和马丁格尔残差都可用于识别异常值，即从发生相关事件到事件发生的时间比模型预测的时间要长得多，或者发生相关事件的时间比模型预测的时间要早得多。对于这些残差，大的阳性预测值代表比模型预测值更早经历相关事件的个体，而阴性预测值则代表比模型预测值更长时间 "存活 "到相关事件的个体。这两组残差的主要区别在于它们的分布和偏斜度。马丁格尔残差的理论最大值为 +1，但可以出现任意大小的阴性预测值，从而产生看似异常值（存活时间长于预测值的个体）但实际并非异常值的值。因此，建议使用离差残差。这些值更均匀地以零为中心，正负两个方向的值分布更均匀。

当对时间绘制残差图时，舍恩费尔德残差也可以用来识别数据中的异常值，但这些残差实际上是用来发现对模型中参数影响较大的观测值。与缩放舍恩费尔德残差一样，定义模型中的每个参数都有一组残差值。使用 "设置图表格式"对话框，可以循环选择要绘制在生成图表上的特异性残差图。在这些图表中，残差值大表示观测值对所选参数的影响大。

预测因子是线性的吗？

Cox 比例风险回归模型的另一个假设是对数（风险率）与参数估计之间存在线性关系。回顾一下，Cox 比例风险回归的模型是：

或者换一种方法：

 

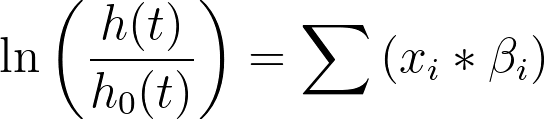
在这种安排下，可以看出每个 β 值都应与对数（危险率）呈线性关系。通过绘制 Deviance 或 Martingale 残差与预测变量值的对比图，可以对这一线性假设进行研究。对于线性预测变量来说，无论预测因子的值如何，这些残差都应大致以零为中心。观察不同预测因子变量值的残差趋势，可能会发现偏离线性的情况。与使用偏差残差和马丁格尔残差检查数据中的异常值一样，在检查预测因子变量的线性时，也建议使用偏差残差，因为它们在零点附近的分布更均匀。

拟合优度如何？

Prism 为 Cox 比例风险提供的最后一种残差图是累积风险率的 Cox-Snell 残差与 Nelson-Aalen 生存估计器。与Kaplan-Meier 生存函数估计器一样，累积危害函数的 Nelson-Aalen 估计器也是累积危害率的非参数估计器。Cox-Snell 残差的定义如下：

 

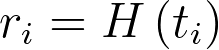
换句话说，观察值 i 的 Cox-Snell 残差等于该观察值的累积危险估计值（该值由 Prism 报告在结果的 "个体价值"选项卡上）。

我们的想法是，如果模型与数据拟合值良好，则将 Cox-Snell 残差图（模型估计的累积危险度值）与累积危险度的 Nelson-Aalen 估计器（非参数估计）绘制成一条直线。拟合优度良好的模型实际上就是这种情况，这些图形经常被用来证明拟合优度。但有一个问题！许多研究报告都指出，如果模型的拟合度特别差，Cox-Snell 残差与累积危险度的 Nelson-Aalen 估计值的对比图就不可能是大致线性的。换句话说，仅仅因为该图生成了一条直线，并不能证实该模型与数据拟合得很好。