如果将 "加权 "选项卡上的选择设置为默认值--不加权--当散点实际与 Y 值相关时,会发生什么情况?答案当然是 "依赖度"?依赖度取决于散点有多大,以及 Y 值的跨度范围有多大。本文接下来将介绍一个本示例,并模拟多个数据集,看看拟合不当会出现什么情况。
模拟
我选择了一个非常简单的模型--一条直线。我对数据进行了模拟,使直线上任意一点的散点 SD 与该点的 Y 值成正比。下图显示了一个模拟数据集。您可以清楚地看到,随着直线的上升,重复样本间的散度也在增加。
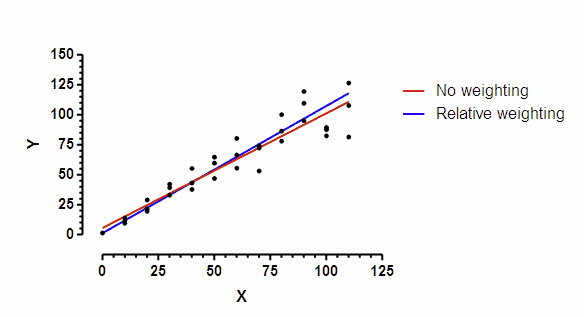
这条线是通过 "非线性 "回归与数据拟合的。作为线性回归分析的一部分,Prism 不提供差分加权,但 "非线性 "回归可以用线性回归分析中没有的许多选项拟合出一条直线。
红线使用默认选项--不加权;最小化平方和。蓝线使用了相对权重。当你希望重复残差的 SD 与 Y 成正比时,这种选择是合适的。
我使用 Prism 的蒙特卡洛分析模拟了 5000 个这样的数据集。对 5000 个模拟数据集中的每个数据集都进行了非加权和加权(相对权重)回归拟合。我同时记录了对这 5000 个数据集进行的两种分析的斜率拟合优度值及其标准误差 (SE)。
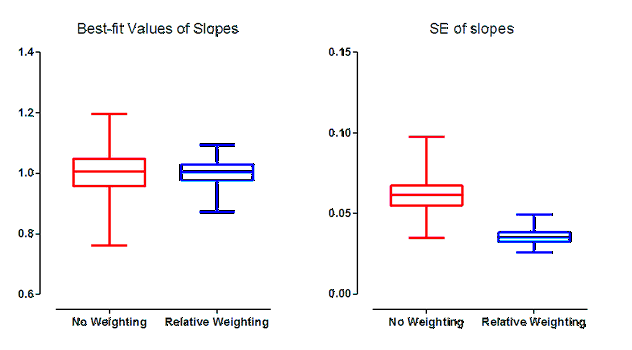
重复样本之间的散度与 Y 成正比,因此相对权重是合适的。模拟结果以蓝色显示。红色显示的是使用等权重(默认值)回归时的结果。方框从第 25 个百分位数延伸到第 75 个百分位数,并在中位数(第 50 个百分位数)处划线。胡须向下延伸到最小值,向上延伸到最大值。
上图左侧显示了斜率拟合优度值的分布。选择错误的加权方案不会系统性地导致斜率的拟合优度值过高(过陡)或过低(过浅)。事实上,无加权拟合和相对权重拟合的斜率最佳拟合值中位数几乎相同。但要注意的是,无加权拟合结果的斜率分布范围更广。由于这些都是模拟数据,我们知道真实的斜率(1.0),因此可以量化每个模拟数据集的最佳拟合斜率与该想法的距离。在不进行差分加权(红色)拟合数据时,误差中位数为 0.04610,而在进行相对权重(蓝色)模拟时,误差中位数为 0.02689.在本示例中,选择错误的加权方案使误差中位数增加了 71%。
上图右侧显示了斜率 SE 的分布。在对所有点进行等权重拟合时,斜率 SE 的平均值要高得多,而且一致性较差(分布较广)。未加权拟合的 SE 中值比加权拟合的 SE 中值大 73%。由于置信区间的宽度与 SE 成正比,这意味着在未加权拟合时,置信区间的中位数要宽 73%。
由于这些是模拟数据,我们知道真实的群体斜率(为 1.0)。因此,我们可以询问每次模拟所报告的 95% 置信区间是否包含真实值。对于相对权重模拟,95.3% 的模拟数据集的 95% 置信区间包含真实值。而在没有加权的情况下分析同样的数据集时,只有 92.6% 的 "95%"置信区间包含真实值。
总结
综上所述,当我们在本示例中选择了错误的加权方案时:
•斜率的拟合优度值不够精确。
•斜率的 SE 值更大,因此置信区间更宽。
•即使 95% 置信区间更宽,但还不够宽。95%"置信区间只包含了不到 95% 模拟中的真实值。
这只是本示例之一。在其他本示例中,加权方法的选择并不那么重要。但对于其他本示例,它可能更重要。值得尝试选择合适的加权方案。