逻辑一词有三个含义，相互之间关系不大 (1)。

含义 1：逻辑人口增长

'逻辑增长"一词最早发明于 19 世纪，用于描述人口增长曲线。 这个概念非常简单。人口增长是有限的，因此永远不会超过某个我们称之为 Nmax 的值。 任何时间 t 的人口变化率都与当时活着的个体数量（Nt）成正比。但人口增长速度在达到最大值时会减慢，因此也与（Nmax - Nt）成正比。因此，人口变化率与 Nt（Nmax - Nt）成正比。

将该微分方程积分，得到的结果称为对数方程。它定义了一条西格玛形曲线，该曲线定义了任何时间的人口数量。该模型有三个参数：起始种群、最大种群和达到半最大种群所需的时间。有时会对其进行修改，增加第四个参数来定义曲线的陡度。

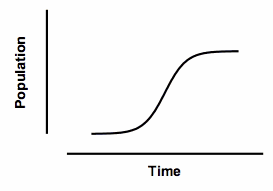
这条曲线过去曾被人口学家使用，但实际上并不能很好地描述人类人口的增长。但它仍被用于模拟肿瘤的增长，以及模拟使用新产品（如手机）的人口比例。

该模型还用于自催化反应，即反应产物也是该反应的催化剂。在这种反应中，产物的积累速度与已经生成的产物浓度乘以剩余底物浓度成正比。这与种群增长模型的数学形式相同。除了 Y 轴是酶反应产生的产物浓度（而不是种群）之外，该图与上图完全相同。

含义 2："逻辑"剂量反应曲线

Bindslev 回顾了许多用于描述剂量反应曲线方程的历史(2)。一个基于希尔研究的常用方程将反应定义为最小反应、最大反应、唤起最小反应和最大反应之间一半反应所需的浓度（EC50）以及描述曲线陡峭程度的参数的函数。 在 Prism 中，该方程称为 log（激动剂）vs 反应曲线--变异性斜率（四个参数）。

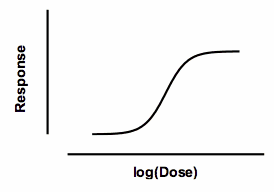
任何剂量下的反应都由一个包含四个参数的等式来定义：最小反应、最大反应、log(EC50) 和斜率因子（也称为 Hill 斜坡）。令人惊讶的是，这个方程的数学形式与描述种群增长的逻辑方程相同，尽管两者的用途完全不同。因此，剂量反应方程有时也被称为 "对数"方程。由于有四个参数，有时也称作四参数逻辑方程，简称 4PL。

这种剂量反应模型可以描述许多系统，但它纯粹是经验性的。它与任何分子模型都不对应（也许，Hill 斜率为整数时除外）。

请注意用逻辑生长方程来描述种群增长，与用它来描述剂量反应曲线之间的巨大差异。

•人口增长曲线的 X 轴是时间。剂量反应曲线的 X 轴是剂量或浓度的对数轴。

•种群生长方程来自理论。剂量反应关系的方程是经验公式。

•尽管名称如此，但人口增长的逻辑方程中并没有使用对数。对数剂量反应曲线的 X 轴是剂量或浓度的对数。

含义 3：逻辑回归

逻辑 这个词的第三种用法，与其他两种用法完全无关，是逻辑回归。这是当结果（依赖度）有两种可能结果时使用的多元回归方法。当模型只有一个预测因子变量时，称为"简单逻辑回归"，而包含多个预测因子变量的模型称为"多元逻辑回归"。方程的意义在于从一组自变量中预测结果的概率 P。为了创建一个始终预测 P 值介于 0 和 1 之间的模型，逻辑回归模型实际预测的是几率的自然对数。 根据几率计算几率自然对数的函数称为logit函数（读作 "长 O "和 "软 G"），因此用于预测来自多个独立变量的概率的 logit 的回归称为 逻辑回归。

参考文献

1.J.S. Cramer.Logit 模型的起源与发展。经济学和其他领域的 Logit 模型》第 9 章，剑桥大学出版社，2003 年。

2.N. Bindslev,Hill in Hell(pdf), Chapter 10 ofDrug-Acceptor Interactions, ISBN: 978-91-977071-0-7