什么是线性回归？

线性回归将这一模型与您的数据相匹配：

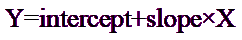
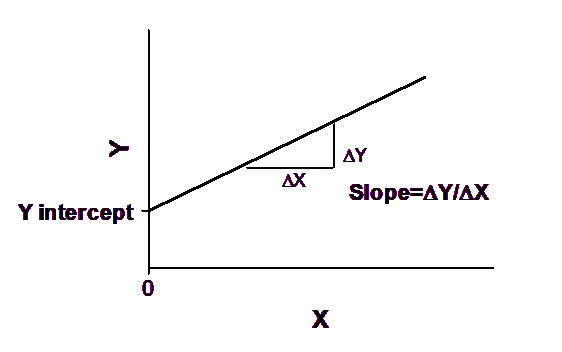
斜率表示直线的陡度。它等于 X 轴每变化一个单位时 Y 轴的变化量，用 Y 轴的单位除以 X 轴的单位来表示。如果斜率为正，则 Y 随 X 的增加而增加。如果斜率为负值，则随着 X 的增加，Y 值减小。

Y 截距是 X 等于零时直线的 Y 值。它定义了直线的高程。

相关性和线性回归并不相同。回顾两者的区别。

简单线性回归与多元线性回归

简单线性回归如上图所示。只有一个 X 变异性。而多元线性回归将 Y 定义为包含多个 X 变量的函数。更一般地说，还有其他类型的关系，其中可以使用多个 X 变异性来描述一个 Y 变量。这些方法统称为多元回归（多元线性回归是多元回归的一种），您可以在此阅读更多有关多元回归原理的内容。

线性回归与逻辑回归

在简单线性回归中，因变量（Y）是连续的，这意味着它可以取任意范围的值。在某些情况下，Y 变量可能不是连续性的。例如，如果您的 Y 变量只能是两个值中的一个（例如，是或否、头或尾、雄性或雌性小鼠等），那么就可以说它是二元分类变量。在这种情况下，线性回归是不合适的。相反，您可以考虑使用逻辑回归，它可以模拟观察到给定结果（有时称为 "成功"）的概率。与线性回归一样，逻辑回归也可以使用一个或多个 X 变量。请阅读有关简单逻辑回归（只有一个 X 变异性）和多元逻辑回归（有多个 X 变异性）的更多信息。