尽管非线性回归，顾名思义，是为拟合非线性模型而设计的，但有些推论实际上假定模型的某些方面接近线性，因此每个参数值的不确定性是对称的。

对方程重新参数化可以使不确定性更加对称，使 SE 更容易解读，也使对称渐近 CI 更有帮助。Prism 可以计算非对称 CI，当您选择这种方法时，如何对方程进行参数化就不那么重要了。

什么是重新参数化？

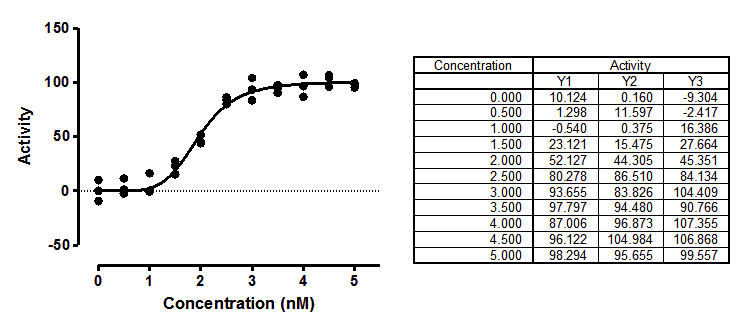
用于将曲线酶动力学数据拟合到标准模型的模型有两种形式：

Y=Vmax*X^h/(Khalf^h + X^h) 

Y=Vmax*X^h/(Kprime + X^h) 

这两个方程是等价的。它们都拟合 Vmax（外推到底物浓度非常高时的最大活性）和 h（Hill 斜率，描述曲线的陡峭程度）。但一个模型拟合的是 Khalf（获得最大速度一半所需的浓度），另一个模型拟合的是 Kprime（底物作用的一种更抽象的测量方法）。

哪个模型最好？两者是等价的，Kprime 等于Khalfh，因此它们会生成完全相同的曲线。

由于平方和将完全相同，自由度也将完全相同，因此，无论您选择这种模型的哪种形式，对这种模型和另一种模型进行任何比较都将得到完全相同的结果。

参数分布并不总是对称的

模拟可以确定参数不确定性的对称程度。我用 Vmax=100、h=5、Kprime=25（所以 Khalf=5）和 SD 等于 7.5 的高斯散射模拟了西格玛酶动力学。X 值与上图相符，每个 X 处的 Y 值为三份。我重复模拟了 5000 次，将每条曲线都拟合为两种形式的模型，并将 Kprime 和 Khalf 的拟合优度值列表，还计算了各自的偏斜度。

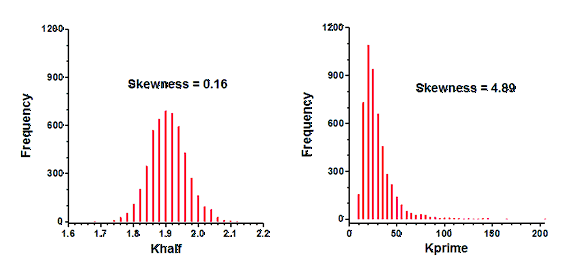
显然，Khalf 的分布相当对称，看起来是高斯分布。偏斜度接近零，符合对称分布的预期。相比之下，Kprime 的分布则相当偏斜度。请注意，有几次模拟的 Kprime 拟合优度值大于 100。偏斜度值（4.89）证实了通过观察可以明显看出的情况--分布远非对称。

用霍加尔偏斜度量化不对称现象

上述结果是通过多次模拟计算得出的。还有一种更简单的方法来计算参数的对称性。Prism 可以计算每个参数的霍加偏斜度，计算公式、数据点数量、X 值间距和参数值。对于模拟数据集，Khalf 的霍加偏斜度为 0.09，Kprime 的霍加偏斜度为 1.83。一个经验法则是，当霍加德偏斜度的绝对值大于 0.25 时，期望值会出现不对称问题；当该值大于 1.0 时，期望值会出现大问题。这些值可以通过一个没有模拟的数据集计算出来，它们告诉你，当你拟合 Khalf 时，对称置信区间会比拟合 Kprime 时更准确。

请注意，虽然 Prism 6 和 7 可以正确计算非加权拟合的 Hougaard 偏斜度，但如果您选择不等加权，它们的计算就会出错。Prism 8 修正了这一问题。

不对称参数的后果

理想情况下，置信区间易于解读。95% CI 有 95% 的概率包含参数的真实人口值，5% 的概率缺失参数值。

在分析真实数据时，我们永远不知道真实参数的值，因此永远不知道区间是否包含它。但模拟数据时，我们知道参数的真实值，因此可以量化置信区间的覆盖范围。我设置了上述相同的模拟，将每个数据集拟合到两个等式中，并将每个置信区间是否包含真实参数值列表。该表显示了在 5000 次模拟中，渐近对称置信区间不包括真实参数值的部分（Kprime 为 25，Khalf 为 1.9037）。

这些结果表明，鉴于 Khalf 的对称性（见上文），Khalf 表现良好。95% 的置信区间期望值在 5.0% 的模拟中缺失真实值。事实上，只有 5.1% 的情况会出现这种情况。同样，期望值为 99% 的置信区间会在 1.0% 的模拟中缺失真实值，事实也正是如此。相比之下，Kprime 的表现就没那么好了。计算出的 95% 置信区间不够宽，因此在 8.8% 的模拟中缺失了真实值。99% 置信区间同样不够宽，因此有 4.8% 的模拟结果缺失了真实值。因此，计算得出的置信区间为 99%，实际结果为 95%。

这些模拟显示了选择适合 Khalf 的方程而不是适合 Kprime 的方程的优势。Khalf 的分布是对称的，因此根据这些拟合值计算出的置信区间可以按表面值来解读。相比之下，Kprime 的分布不对称，其置信区间不能从表面价值来解读。

如果要求 Prism 呈现非对称剖面似然置信区间，参数化并不重要

如果选择不对称剖面似然置信区间，那么选择哪种形式的方程并不重要。两种情况下的覆盖率是一样的，都非常接近 95% 或 99%。有了这个选择，你就可以选择符合教科书和论文的方程形式，或者符合你的思维方式的方程形式。如果你喜欢图形思维，请选择 Khalf。如果你喜欢机械地思考，请选择 Kprime。