为什么不应该使用R2来比较模型

R2可以量化模型与数据的拟合程度，因此似乎是比较模型的一种简单方法。听起来确实很简单--选择R2 较大的模型。这种方法的问题在于，添加更多参数不会受到惩罚。因此，拥有更多参数的模型会弯曲和扭曲得更多，从而更接近点，因此几乎总是拥有更高的R2。如果将R2作为选择最佳模型的标准，那么几乎总是会选择参数最多的模型。

调整后的R2考虑了拟合参数的数量

调整后的R2值总是低于R2（除非您只拟合一个参数）。下面的等式说明了原因。

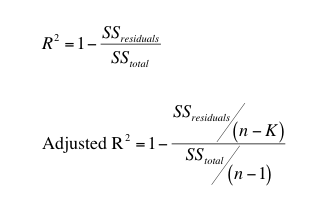
上式显示了调整后R2的计算方法。回归线或回归曲线的残差平方和有 n-K 个自由度，其中 n 是数据点数，K 是回归拟合的参数数。总平方和是通过所有 Y 均方值的水平线的距离平方和。由于它只有一个参数（均值），因此自由度等于 n-1。

当 K=1 时，调整后R2与普通R2相同。当 K>1 时，调整后R2小于普通 R2。

使用调整后的R2和快速简便的模型比较方法

比较模型的快速简便方法似乎是选择调整后R2 较小的模型。选择在 "诊断"选项卡上报告该值。

用调整后R2比较模型是比较多元线性回归拟合模型的标准方法。但它不是非线性回归的标准方法是有原因的。Speis 和 Neumeyer(1)进行的模拟显示，使用调整后的R2是在竞争模型中进行选择的可怕方法。我们建议您使用平方和外 F 检验或比较 AICc。如果您确实通过比较调整后的R2 来比较模型，请确保所有拟合都使用了相同的数据和相同的加权。但即便如此，也要知道，根据 AICc 评估的拟合值非常不同的模型，其R2值可能仅在小数点后第三位至第五位数字（1）之间存在差异。

线性回归中的调整R2

Prism 不会报告线性回归的调整后R2，但可以用非线性回归拟合直线。

如果 X 和 Y 完全没有线性关系，则最佳拟合斜率预计为 0.0。如果对许多随机抽样的样本进行分析，一半样本的斜率为正，一半样本的斜率为负。 但在所有这些情况下，R2都将为正（或零）。R2绝不可能为负（除非您对斜率或截距进行了限制，使其被迫拟合得比水平线更差）。 相反，调整后的R2可以是负值。如果您分析了许多随机抽样的样本，您会发现调整后的R2在一半样本中为正，而在另一半样本中为负。

这里有一个简单的区分方法。R2量化了您正在分析的数据样本中的线性关系。即使没有潜在的关系，该样本中也几乎肯定存在某种关系。调整后的R2比R2小，是对潜在群体中关系程度的最佳估计。

 Spiess, A.-N. & Neumeyer, N.An evaluation of R2 as an inadequate measure for nonlinear models in pharmacological and biochemical research: a Monte Carlo approach.BMC Pharmacol 10, 6-6 (2010).