稳健回归的必要性

非线性回归和线性回归一样，都假设理想曲线周围的数据散点服从高斯分布或正态分布。这一假设引出了我们熟悉的回归目标：最小化各点与曲线之间的垂直距离或 Y 值距离的平方和。这种进行非线性（或线性回归）的标准方法称为最小二乘回归。

实验错误会导致错误值，其值过高或异常值过低。即使是一个异常值，也会在平方和计算中占主导地位，并导致误导性结果。解决这一问题的方法之一是使用对违反高斯假设不十分敏感的方法进行稳健拟合。另一种方法是使用自动异常值消除来识别和移除异常值，然后运行最小二乘回归。Prism 提供这两种选择。异常值识别方法实际上是先进行稳健拟合，这样就有了一个基线，可以据此判断某个点何时偏离基线过远，从而被定义为异常值。然后在剔除异常值后，对剩余的点进行标准的最小二乘拟合。

稳健回归的工作原理

根据 Numerical Recipes (1) 中的建议，我们的稳健拟合方法基于以下假设：曲线周围的变化服从洛伦兹分布，而不是高斯分布。这两种分布都属于 t 分布族：

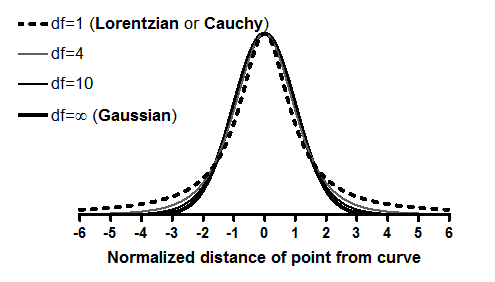
图中最宽的分布，即 df=1 时的 t 分布，也称为洛伦兹分布或柯西分布。洛伦兹分布的尾部较宽，因此异常值相当常见，因此对拟合影响不大。

我们调整了马夸特非线性回归算法，以适应残差的洛伦兹（而非高斯）分布假设，并在参考文献 2 中解释了细节。

何时选择稳健非线性回归有意义？

在 Prism 中，稳健回归的主要用途是作为 "基线"，从中剔除异常值。您可能想尝试使用稳健回归，以便更好地理解异常值去除方法（始于稳健回归）。如果您的唯一目标是从标准曲线进行插值，而该标准曲线有一个或多个异常值，您可能也会发现它很有用。

我们建议您在大多数情况下避免使用稳健回归（至少是 Prism 实现的稳健回归），因为它有以下缺点：

•稳健回归无法计算参数的标准误差或置信区间。

•稳健回归无法绘制置信带或预测带。

•鲁棒回归无法计算参数相互交织的程度。无法计算协方差矩阵或依赖度值。

•稳健回归无法比较两个模型或两个数据集的拟合程度。

无法比较模型在大多数情况下并不重要。但无法提供诊断信息（SE、CI、协方差矩阵、依赖度、置信带和预测带）严重限制了稳健回归对大多数研究的实用性。

 

参考文献                                                                         

1.Press WH, Teukolsky SA, Vettering WT, Flannery BP: Numerical Recipes in C. the Art of Scientific Computing. 纽约州纽约市：剑桥大学出版社；1988 年。

2.Motulsky HM and Brown RE, Detecting outliers when fitting data with nonlinear regression - a new method based on robust nonlinear regression and the false discovery rate, BMC Bioinformatics 2006, 7:123. 以 pdf 格式下载。